Star in a regular pentagon
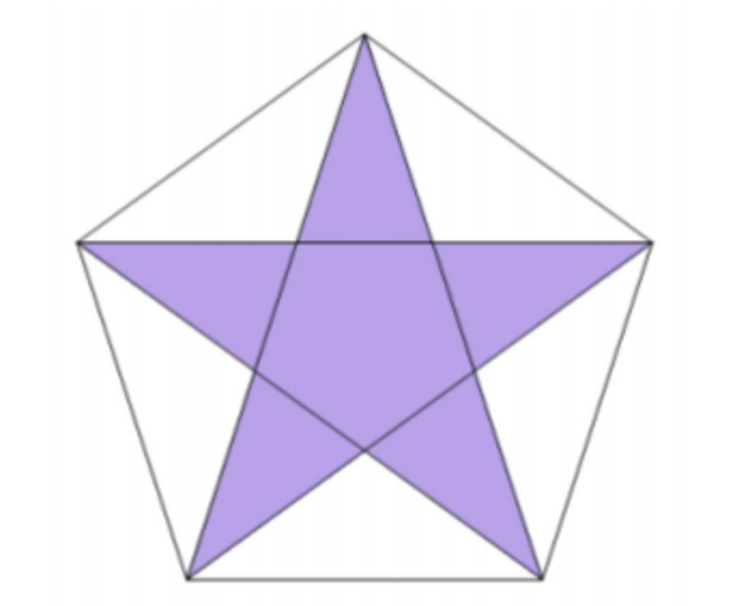 In a regular pentagon the diagonals are joined to form a star.
In a regular pentagon the diagonals are joined to form a star.
The star occupies approximately what % of the pentagon?
The answer is 47.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
|
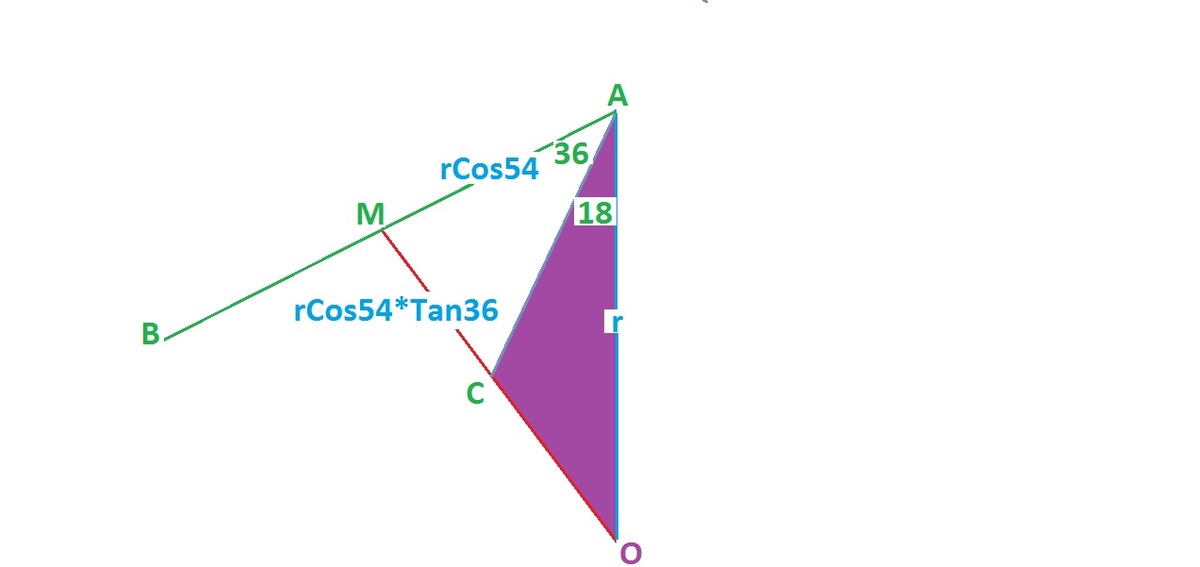 AB is the side of the pentagon. M its midpoint. O the center
and AO=r.
r
i
g
h
t
∠
d
Δ
A
M
O
=
1
0
1
o
f
t
h
e
P
o
l
y
g
o
n
.
Δ
A
M
C
=
1
0
1
o
f
u
n
s
h
a
d
e
d
a
r
e
a
.
The angles in the sketch are from pentagon properties.
Sides are from trigonometry.
A
r
e
a
Δ
A
M
C
=
2
1
∗
r
C
o
s
5
4
o
∗
(
r
C
o
s
5
4
o
∗
T
a
n
3
6
o
)
A
r
e
a
Δ
A
M
O
=
2
1
∗
r
C
o
s
5
4
o
∗
r
S
i
n
(
1
8
o
+
3
6
o
)
.
F
r
a
c
t
i
o
n
o
f
s
t
a
r
=
1
−
A
r
e
a
Δ
A
M
O
A
r
e
a
Δ
A
M
C
=
2
1
∗
r
C
o
s
5
4
o
∗
r
S
i
n
5
4
o
2
1
∗
r
C
o
s
5
4
o
∗
r
(
C
o
s
5
4
o
∗
T
a
n
3
6
o
)
=
1
−
C
o
t
5
4
o
T
a
n
3
6
o
=
1
−
(
T
a
n
3
6
o
)
2
%
=
4
7
.
2
AB is the side of the pentagon. M its midpoint. O the center
and AO=r.
r
i
g
h
t
∠
d
Δ
A
M
O
=
1
0
1
o
f
t
h
e
P
o
l
y
g
o
n
.
Δ
A
M
C
=
1
0
1
o
f
u
n
s
h
a
d
e
d
a
r
e
a
.
The angles in the sketch are from pentagon properties.
Sides are from trigonometry.
A
r
e
a
Δ
A
M
C
=
2
1
∗
r
C
o
s
5
4
o
∗
(
r
C
o
s
5
4
o
∗
T
a
n
3
6
o
)
A
r
e
a
Δ
A
M
O
=
2
1
∗
r
C
o
s
5
4
o
∗
r
S
i
n
(
1
8
o
+
3
6
o
)
.
F
r
a
c
t
i
o
n
o
f
s
t
a
r
=
1
−
A
r
e
a
Δ
A
M
O
A
r
e
a
Δ
A
M
C
=
2
1
∗
r
C
o
s
5
4
o
∗
r
S
i
n
5
4
o
2
1
∗
r
C
o
s
5
4
o
∗
r
(
C
o
s
5
4
o
∗
T
a
n
3
6
o
)
=
1
−
C
o
t
5
4
o
T
a
n
3
6
o
=
1
−
(
T
a
n
3
6
o
)
2
%
=
4
7
.
2
Am I suppose to use the calculator??
Yes, to divide tan(36) over tan(54)
Log in to reply
tg(36°)/tg(54°)=tg(36°) x tg(36°),no need for dividing...
Log in to reply
then what ?
Log in to reply
@Abdulrahman El Shafei – this was good one !! try my "probably this one!!!"
Let us consider one-fifth of the pentagon. Let the center of the pentagon by O , the side of the pentagon be a , two adjacent vertices of the pentagon be A and B , and the other vertex of the non-shaded triangle be P .
We note that ∠ O A B = 5 4 ∘ and ∠ P A B = 3 6 ∘ . And the area of △ O A B = 5 1 of the area of pentagon is given by:
A O A B = 2 1 a ( 2 1 a tan 5 4 ∘ )
Similarly, he area of △ P A B = 5 1 of total non-shaded area is:
A P A B = 2 1 a ( 2 1 a tan 3 6 ∘ )
Therefore, the portion of non-shaded area is:
A P A B A O A B = tan 5 4 ∘ tan 3 6 ∘
The portion the star occupies:
1 − A P A B A O A B = 1 − tan 5 4 ∘ tan 3 6 ∘ = 1 − 1 . 3 7 6 3 8 1 9 2 0 . 7 2 6 5 4 2 5 2 8
= 0 . 4 7 2 1 3 5 9 5 5 ≈ 4 7 . 2 %