$x > x^2$

Computer Science Level 3

Let $S(n)$ denote the sum of the digits of an positive integer $n$ .

Find the smallest positive integer $x$ such that $S(x)>S(x^2)$ .

The answer is 39.

8 solutions

Brock Brown
Mar 17, 2015

Python 2.7:

def s(n):
    return sum([int(c) for c in str(n)])
def goal(n):
    return s(n) > s(n*n)
n = 0
while not goal(n):
    n += 1
print "Answer:", n

I'm curious about whether the set of all $x$ such that $S(x) \gt S(x^{2})$ is finite or infinite. A proof would need some number theory, but I'm wondering if your program can be adapted to find higher values up to a set limit, just to get an idea of how common such $x$ are.

Brian Charlesworth - 6 years, 2 months ago

The set is infinite.

Hint: There is a very obvious family of solutions, starting with 39.

Hint: What is $10^2$ ?

Calvin Lin Staff - 6 years, 2 months ago

But $S(10^{n}) = S(10^{2n})$ for all non-negative integers $n$ , and we are looking for $x$ such that $S(x) \gt S(x^{2})$ .

Brian Charlesworth - 6 years, 2 months ago

@Brian Charlesworth – Obviously my hints are not immediately applicable.

There is a small intermediary step.

Calvin Lin Staff - 6 years, 2 months ago

@Calvin Lin – Got it. Should have thought for a few more seconds before commenting. :P

Brian Charlesworth - 6 years, 2 months ago

I still dont get it. Lol. Would you mind explaining a little more?

Trevor Arashiro - 6 years, 2 months ago

@Trevor Arashiro – We would have $S(39*10^{n}) = S(39)$ and $S((39*10^{n})^{2}) = S(39^{2} * 10^{2n}) = S(39^{2})$ for any non-negative integer $n$ , since all we would be doing is adding $0$ 's at the end and hence not changing the digit sum.

Thus since $S(39) \gt S(39^{2}),$ we have $S(39*10^{n}) \gt S((39*10^{n})^{2})$ for all non-negative integers $n$ , making the set of all such $x$ infinite. The next question would be: are there an infinite number of distinct solution "families", i.e., an infinite number of "base" numbers such as $39$ that are not multiples of $10$ of one another?

Brian Charlesworth - 6 years, 2 months ago

@Brian Charlesworth – Once again, there is an obvious family of solutions to try. In fact, there are infinitely many families of solutions, all starting with 39, and not containing a multiple of 10. We can make each of these families disjoint (with the exception of the initial term 39).

Hint: If something works, don't break it.

Hint: What is $1000 ^2$ ?

Calvin Lin Staff - 6 years, 2 months ago

@Brian Charlesworth – For clarity, the sequence that I'm referring to is

$39, 3900039, 3900000039, 39000000039, \ldots$

where we add enough 0's so that the cross terms do not matter (and can only help). We could also use terms like 39000003900000000000000039, for variety.

Calvin Lin Staff - 6 years, 1 month ago

The set of all $x$ is looking pretty infinite to me.

Have fun!

Python 2.7:

# prints valid values of x
# until it gets tired
from time import time
seconds = 60
end = time() + seconds
def s(n):
    return sum([int(c) for c in str(n)])
def goal(n):
    return s(n) > s(n*n)
n = 0
while time() <= end:
    if goal(n):
        print n
    n += 1
print "Made it!"

Brock Brown - 6 years, 2 months ago

Hahaha. "#until it gets tired". :) Thanks for doing this. At least now I know that infinite is the likely target.

Brian Charlesworth - 6 years, 2 months ago

Please look if there is any number theory approach and please post it.

Kalpok Guha - 6 years, 2 months ago

Can you post a more efficient solution here ? Thanks.

Pranjal Jain - 6 years, 2 months ago

Chew-Seong Cheong
Apr 2, 2015

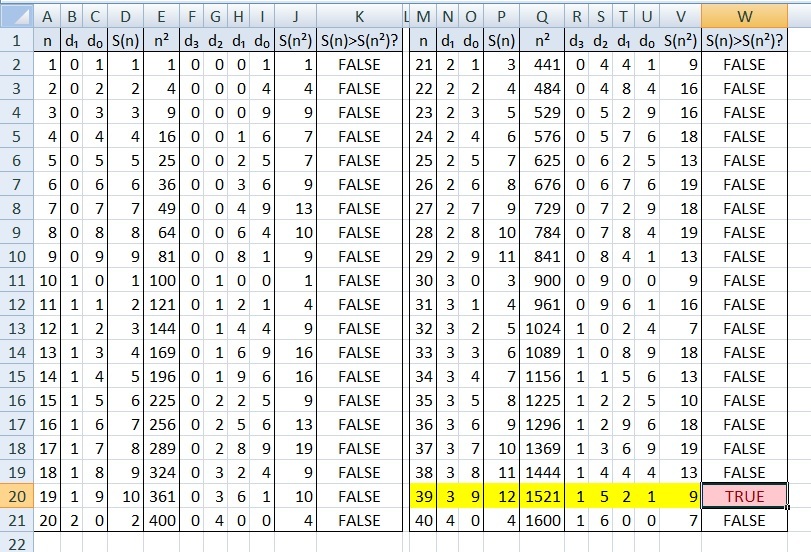
For a change, I decided to use a spreadsheet to do this. The formulas keyed in are as follows:

A2: 1
B2: =INT(A2/10)
C2: =A2-10*B2 
D2: =B2+C2
E2: =A2*A2
F2: =INT(E2/1000)
G2: =INT((E2-1000*F2)/100)
H2: =INT((E2-1000*F2-100*G2)/10)
I2: =E2-1000*F2-100*G2-10*H2
J2: =F2+G2+H2+I2
K2: =D2>J2

To check the required answer with in column K or W, we can use the Conditional Formatting > Highlight Cells Rules > Equal To... > key in "TRUE" > OK.

The answer is found to be $\boxed{39}$ .

Is there no way to arrive to the result mathematically on pen and paper?

Yugesh Kothari - 4 years, 6 months ago

Not that I know of. This is a Computer Science problem.

Chew-Seong Cheong - 4 years, 6 months ago

Tarun Singh
Mar 17, 2015

C language :

#include <stdio.h>
int ds(int i)    
{
    int s=0;
    while(i>=1)
    {
        s+=i%10;
        i=i/10;
    }
    return s;
}
int main(void)
{
      int j;
      for(j=1;j>0;j++)
      {
          if(ds(j)>ds(j*j))
          {
              printf("%d",j);
              break;
          }
      }
}

Abhishek Sharma
Mar 17, 2015

Turbo C++

#include <conio.h>
#include <iostream.h>
#include <math.h>
int s(int num)
{
    int s=0;
    while (num>0)
    {
        s=s+num%10;
        num=num/10;
    }
    return s;
}
void main()
{
    clrscr();
    int i;
    for (i=1;i>0;i++)
    {
        if (s(i)>s(pow(i,2)))
        {
            cout<<i;
            break;
        }
    }
    getch();
}

@Calvin Lin @Ronak Agarwal please post a NT approach.

Adarsh Kumar - 6 years, 2 months ago

There isn't really much to it other than trial and error.

I've moved this problem into CS, since that is the most sensible approach for problems like this.

I just realized that this comment wasn't true, so I edited it. It is now correct.

Calvin Lin Staff - 6 years, 2 months ago

You are absolutely basically I also wrote the problem with trial and error method as I do not know computer science much.I posted it here to know are there any number theory approach and thank you for moving it it's original section.

Kalpok Guha - 6 years, 2 months ago

Weuler Filho
Aug 21, 2015

C++ solution

        #include <bits/stdc++.h>

        using namespace std;

        int sumdigits(int n) {
            int sm = 0;

            while (n > 0) {
                sm += n%10;
                n/=10;
            }

            return sm;
        }

        int main () {

            int i=0;

            while (sumdigits(i) <= sumdigits(i*i)) i++;

            cout << i << endl;

        }

Arulx Z
May 15, 2015

public static void main(String args[]) {
    for(double n = 1;; n++)
        if(sum(n) > sum(n * n)){
            System.out.println(n);
            break;
        }
}

private static double sum(double n){
    int sum = 0;
    while (n != 0) {
        sum += n % 10;
        n /= 10;
    }
    return (double) sum;
}

Kamala Ramakrishnan
Apr 16, 2015

VB.NET solution:

  Module Module1

Sub Main()

    For n = 1 To 1000
        If the_sum(n) > the_sum(n * n) Then
            Console.WriteLine(n)
            Exit For

        End If
    Next
    Console.ReadLine()

End Sub

Public Function the_sum(ByVal number As Integer) As Integer
    Dim sum As Integer = 0
    Dim a As String = number.ToString
    For g = 1 To a.Length
        sum = sum + Val(a(g - 1))
    Next
    Return sum

End Function

 End Module

Andrea Palma
Mar 22, 2015

I found these families

$\begin{array} {| l | l | l | l |} \hline 39 & 390 &3900 & \cdots \\ \hline 399 & 3990 & 39900 & \cdots \\ \hline 3999 & 39990 &399900 & \cdots \\ \hline \vdots & \vdots & \vdots &\vdots \\ \hline \end{array}$

$\begin{array} {| l | l | l | l |} \hline 49 & 490 &4900 & \cdots \\ \hline 499 & 4990 & 49900 & \cdots \\ \hline 4999 & 49990 &499900 & \cdots \\ \hline \vdots & \vdots & \vdots &\vdots \\ \hline \end{array}$

numbers satisfy $S(x)>S(x^2)$ :

39 48 49 79 149 179 249 318 348 349 389 390 399 448 449 480 489 490 498 499 548 549 579 649 679 749 789 790 795 799 849 889 895 898 899 949

Alex Zhong - 6 years, 2 months ago

x > x 2 x > x^2 x > x 2

The answer is 39.

8 solutions

0 pending reports

$x > x^2$