Yellow Area
The base of the pink triangle is one half of the side length of the square.

If the square shown has an area of 12, what is the area of the yellow quadrilateral?
- Inspiration: Daily Challenge
- Bonus: Try to generalize for the area of yellow quadrilateral where the base of the pink triangle is n 1 of the side length s of the square.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
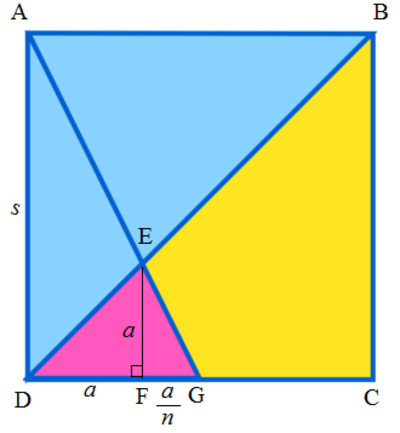
Label the figure as above. Since the side length of the square is s , D G = n s . Let E F be perpendicular to C D . Then △ D E F and △ D B C are similar. If D F = a , E F = D F = a . Also △ E F G and △ A D G are similar. Then E F F G = A D D G = n 1 ⟹ F G = n E F = n a . Now D G = D F + F G = a + n a = n s , ⟹ a = n + 1 s .
Then the area of the pink △ D E G , [ D E G ] = s a ( a + n a ) = 2 n ( n + 1 ) a 2 = 2 n ( n + 1 ) s 2 = 2 n ( n + 1 ) A □ , where A □ = s 2 is the area of the square.
The area of the yellow quadrilateral B C G E , A yellow = [ B C D ] − [ D E G ] = 2 A □ − 2 n ( n + 1 ) A □ = 2 n ( n + 1 ) n 2 + n − 1 A □ .
For n = 2 and A □ , A yellow = 2 ( 2 ) ( 2 + 1 ) 4 + 2 − 1 × 1 2 = 5 .
I've come up with an interesting solution:
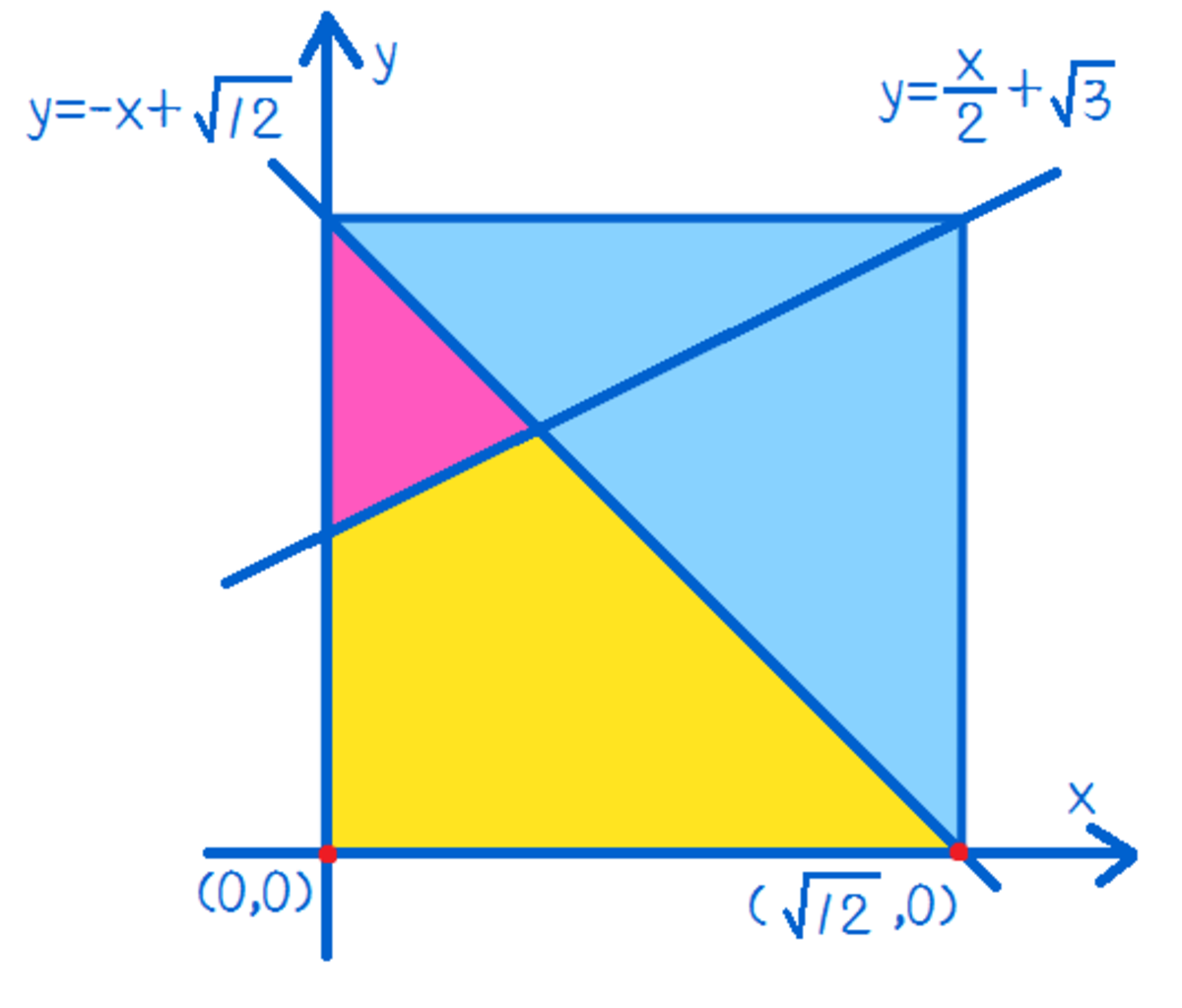
And then the answer is
∫ 0 1 2 min ( 2 x + 3 , − x + 1 2 ) d x
Calculate it, and you get
5
Another way:
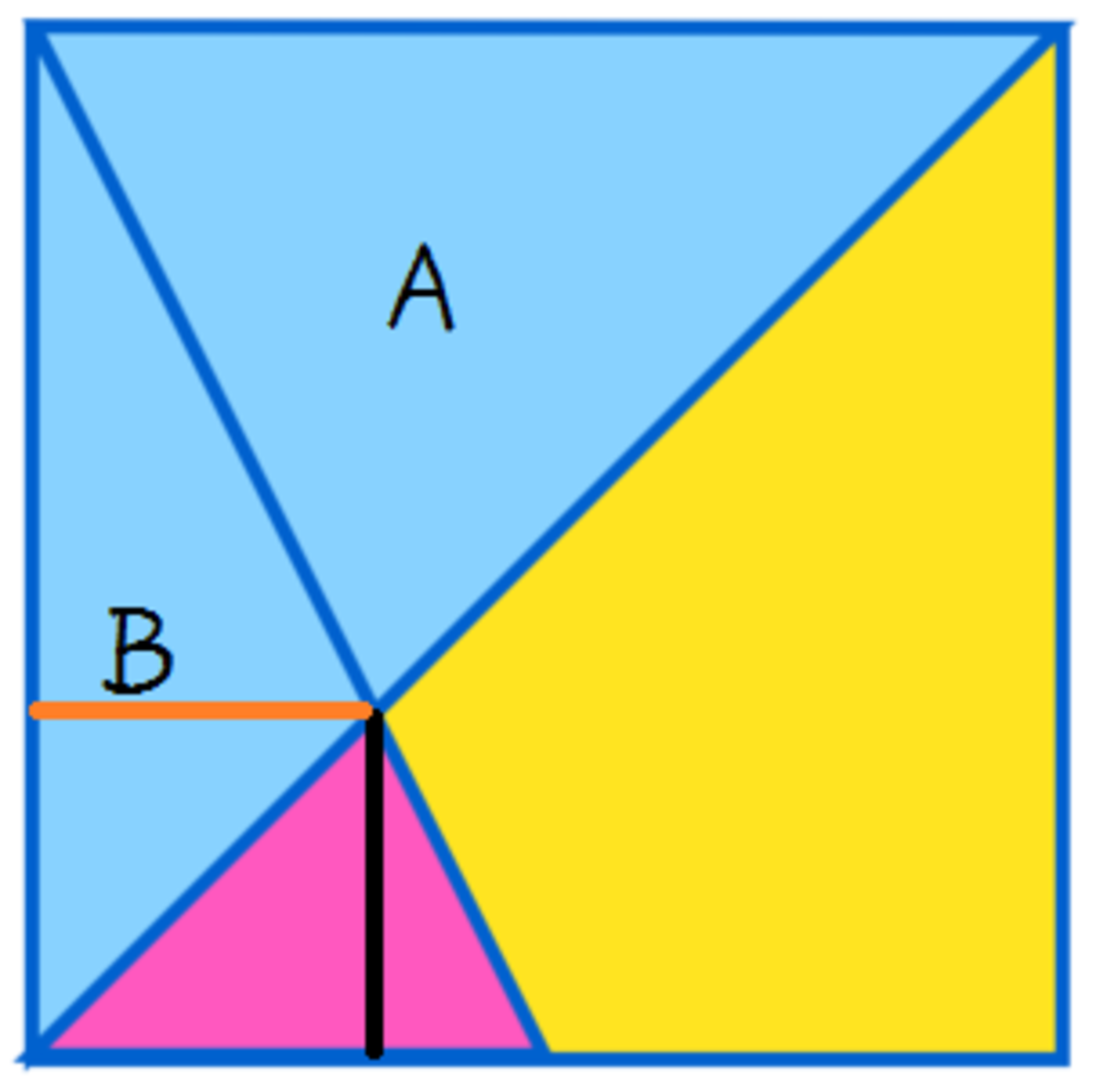
Suppose the blue triangle on the right is A , and the blue triangle on the left is B .
Because the distance from the point on the bisector of the angle to both sides of the angle is equal, the length of the orange line is equal to the length of the black line.
So the area of B is 2 times the area of the pink triangle (the height is equal, and the base is twice).
And because A is similar to the pink triangle, the ratio of the sides is 2 : 1 , so the area ratio is 4 : 1 , that is, the area of A is the pink triangle 4 times.
So the area of the entire big blue triangle (that is, A + B ) is six times that of the pink triangle, and because its area is equal to half the area of the square, which is 6 . So the area of the pink triangle is 1 .
So the area of the yellow triangle is half the area of the square minus the area of the pink triangle:
6 − 1 = 5
For any pink triangle with the base 1/n of the square's side, the yellow quadrilateral is always n²+n-1 times larger.
This can also be solved using coordinate geometry.
Let the bottom left corner of the square be the origin. Then the top left corner of the square has coordinates ( 0 , s ) and the bottom right corner of the pink triangle has coordinates ( n s , 0 ) , and the line through these two points is y = − n x + s . Since the diagonal line has an equation of y = x , these two lines intersect at ( n + 1 s , n + 1 s ) .
Since the pink triangle has a base of n s and a height of n + 1 s , its area is A pink = 2 n ( n + 1 ) s 2 .
Since the yellow quadrilateral is half the square minus the pink triangle, its area is A yellow = 2 s 2 − 2 n ( n + 1 ) s 2 .
In this problem, s 2 = 1 2 and n = 2 , so A yellow = 2 1 2 − 2 ⋅ 2 ( 2 + 1 ) 1 2 = 5 .
 As
B
D
is the diagonal
⇒
area of
b
l
u
e
region
=
2
1
2
=
6
As
B
D
is the diagonal
⇒
area of
b
l
u
e
region
=
2
1
2
=
6
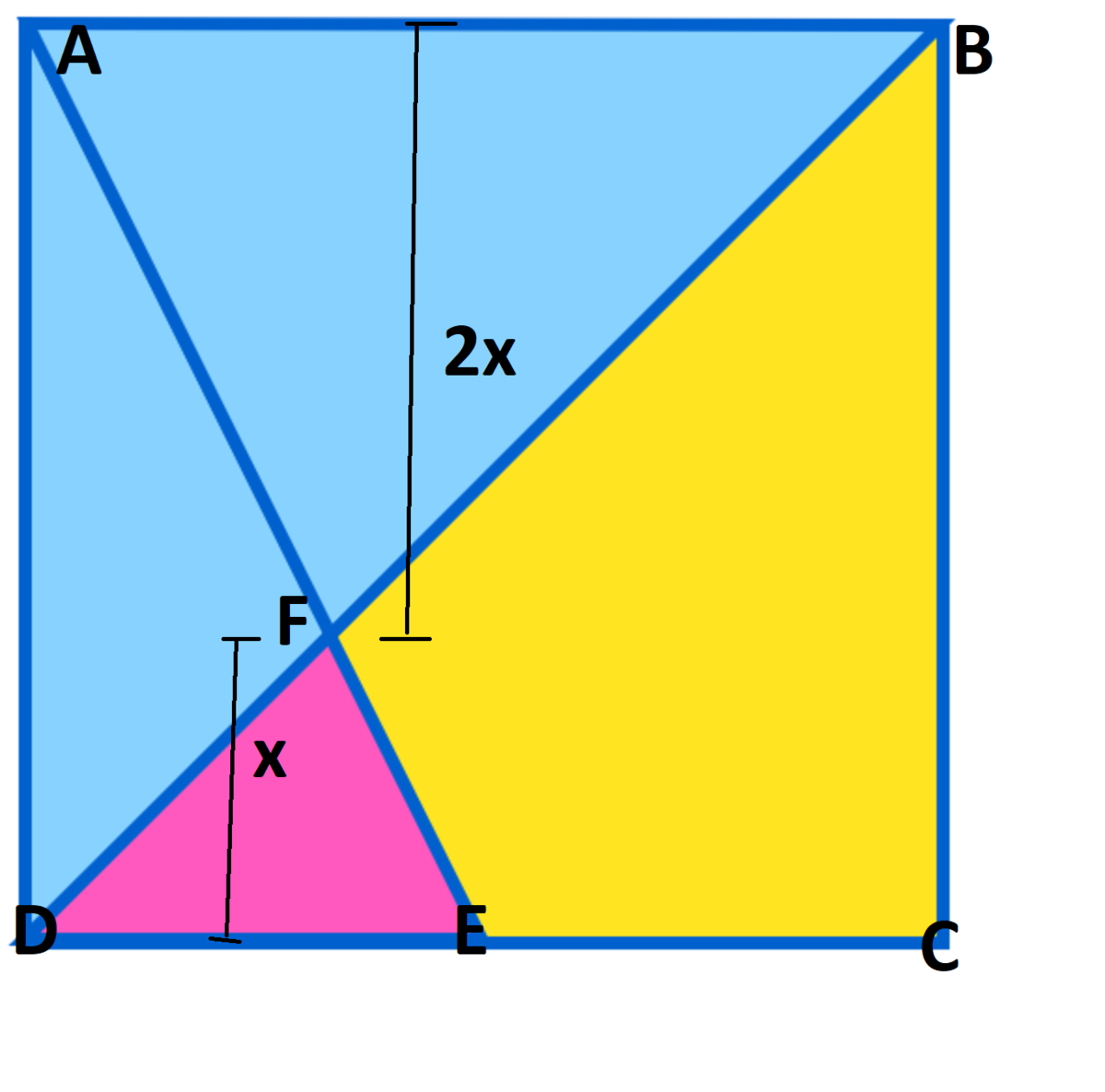
Area of square = A B 2 = 1 2 ⇒ A B = 2 3 = B C
As ∠ D F E and ∠ B F A are opposite to each other ∴ ∠ D F E = ∠ B F A
As A B C D is a square ∴ A B ∣ ∣ C D ⇒ ∠ F D E = ∠ F B A
From the above two statements we deduce that △ F D E ~ △ F B A . . . . . . . [ 1 ]
Let the ratio of the altitude of △ F A B to △ F D E be k
From [ 1 ] : D E A B = k ⇒ 2 = k
Let the altitude of be 0 x
Therefore altitude of △ F A B = 2 x
From the diagram: 2 x + x = A B ⇒ 3 x = 2 3 ⇒ x = 3 2 3
Area of p i n k region = 2 1 3 × 3 2 3 = 3 3 = 1
Area of y e l l o w region = 1 2 − 1 − 6 = 1 2 − 7 = 5
Thanks for the solution, were you able to generalise?
Log in to reply
What type of generalisation? Do you mean for any square with area p ?
Log in to reply
- Bonus: Try to generalize for the area of yellow quadrilateral where the base of the pink triangle is n 1 of the square's side length ( s )
Log in to reply
@Mahdi Raza – The area of the yellow region will always be 5 0 ( 1 − n 2 + n 1 ) % of the whole square. That of pink region will always be 5 0 ( n 2 + n 1 ) %
Log in to reply
@Zakir Husain – Is your answer equivalent to mine (look my solution to bonus)? I am not sure whether it can simplified more. If you think so, please comment and I will elaborate upon that
Log in to reply
@Mahdi Raza – Just multiply the area of pink region by s 2 1 0 0 . And for the yellow area subtract it from 5 0 % + A r e a p i n k % ( 5 0 % for the blue area) and you will get my result.
[Answer to Bonus]
From the preface of this daily challenge , we see that if the base of the triangle is n 1 × s , then it's height will always be n + 1 1 × s . Together the area is:
Pink Triangle = 2 1 ( n 1 ⋅ s ⋅ n + 1 1 ⋅ s ) = 2 ( n ) ( n + 1 ) s 2
Yellow Quadrilateral = 2 s 2 − Pink Triangle = 2 s 2 − 2 ( n ) ( n + 1 ) s 2