Yet another 3-4-5 triangle
Inspiration , along with a few other questions from and inspired by @Fletcher Mattox
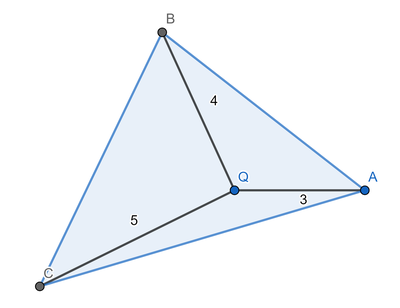
Given a point Q , a triangle Δ A B C is constructed so that A Q = 3 , B Q = 4 , C Q = 5 , as shown in the diagram above. Among all such triangles, what is the largest possible perimeter?
If this perimeter is p , enter ⌊ 1 0 0 0 p ⌋ as your answer.
Bonus: Can you find a closed form for p ?
The answer is 20932.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Can you tell
sympy
to get a closed form of
p
?
It is the largest real root of 3 6 0 0 X 6 − 1 5 6 8 6 3 9 X 4 − 3 8 6 9 2 0 0 X 2 + 1 6 2 5 7 0 2 4 = 0 .
Log in to reply
Not that I am aware of, but apparently Mathematica can. However, I cannot afford that software.
Log in to reply

Log in to reply
Log in to reply
@Pi Han Goh – Let X denote the angle (in radian) sandwiched between the given lengths 4 and 5.
And let Y denote the angle (in radian) sandwiched between the given lengths 3 and 5.
Then we have X , Y ∈ ( 0 , π ) and X + Y > π .
The the perimeter is maximized when ( 3 sin Y 4 sin X ) 2 = 3 4 − 3 0 cos Y 4 1 − 4 0 cos X
or when ( X , Y ) ≈ ( 2 . 2 5 6 7 3 , 2 . 0 6 5 8 2 )
Log in to reply
@Pi Han Goh – Alternatively,
-
let l denote the other length formed from the interior triangle with two given sides 3 and 4
-
let m denote the other length formed from the interior triangle with two given sides 4 and 5
-
let n denote the other length formed from the interior triangle with two given sides 3 and 5
The perimeter is maximized when l 2 + l 2 4 9 + 3 2 = m 2 + m 2 8 1 = n 2 + n 2 2 5 6 + 1 4
or when ( l , m , n ) ≈ ( 5 . 8 4 1 3 1 , 8 . 1 4 4 9 8 , 6 . 9 4 6 2 4 )
Thank you both for sharing your results! @Fletcher Mattox - that's very similar to my approach; I used two variables to represent angles at the centre (essentially your angles B and C; I fixed A=0, because rotating the whole triangle doesn't affect its perimeter), then equated the partial derivatives to zero to find the maximum.
@Pi Han Goh - I went about this numerically (I thought I got close to an analytical solution at one point, but no). That's a wonderful equation you found! I wonder how the coefficients come from 3 , 4 , 5 ?
Log in to reply
Uh-oh...ummm...have we all missed something here? (If so, I feel incredibly stupid for having posted this, because the inspiration problem is actually the solution!!)
Let ∠ B Q C = α , ∠ C Q A = β , ∠ A Q B = γ , so that α + β + γ = 2 π . By the cosine rule,
a 2 b 2 c 2 = B Q 2 + C Q 2 − 2 B Q ⋅ C Q cos α = C Q 2 + A Q 2 − 2 C Q ⋅ A Q cos β = A Q 2 + B Q 2 − 2 A Q ⋅ B Q cos γ
Now, define F ( α , β , γ , L ) = B Q 2 + C Q 2 − 2 B Q ⋅ C Q cos α + C Q 2 + A Q 2 − 2 C Q ⋅ A Q cos β + A Q 2 + B Q 2 − 2 A Q ⋅ B Q cos γ + L ( α + β + γ − 2 π )
(ie set it up as a Lagrangian multiplier problem). Then the partial derivative with respect to α is F α = B Q 2 + C Q 2 − 2 B Q ⋅ C Q cos α B Q ⋅ C Q sin α + L
Equating this and the other partial derivatives to zero (to find the maximum) gives B Q 2 + C Q 2 − 2 B Q ⋅ C Q cos α B Q ⋅ C Q sin α = C Q 2 + A Q 2 − 2 C Q ⋅ A Q cos β C Q ⋅ A Q sin β = A Q 2 + B Q 2 − 2 A Q ⋅ B Q cos γ A Q ⋅ B Q sin γ = − L
We can make two substitutions here; the denominators are just the sidelengths a , b , c ; the numerators are twice the areas of the triangles Δ B Q C , Δ C Q A , Δ A Q B respectively. So the equation becomes
a 2 [ Δ B Q C ] = b 2 [ Δ C Q A ] = c 2 [ Δ A Q B ]
But these are just the heights of the three triangles Δ B Q C , Δ C Q A , Δ A Q B . In other words, the perpendicular distances from Q to the three sides are all the same. In other words, Q is the incentre!
I think I went for numerical methods too quickly with the last one and thought the incentre didn't actually maximise the perimeter.
Have I made a mistake here? Or should I convert this to a solution and be very embarrassed?
Log in to reply
Did you see this ?
Log in to reply
@Fletcher Mattox – I hadn't seen it - but wish I had!
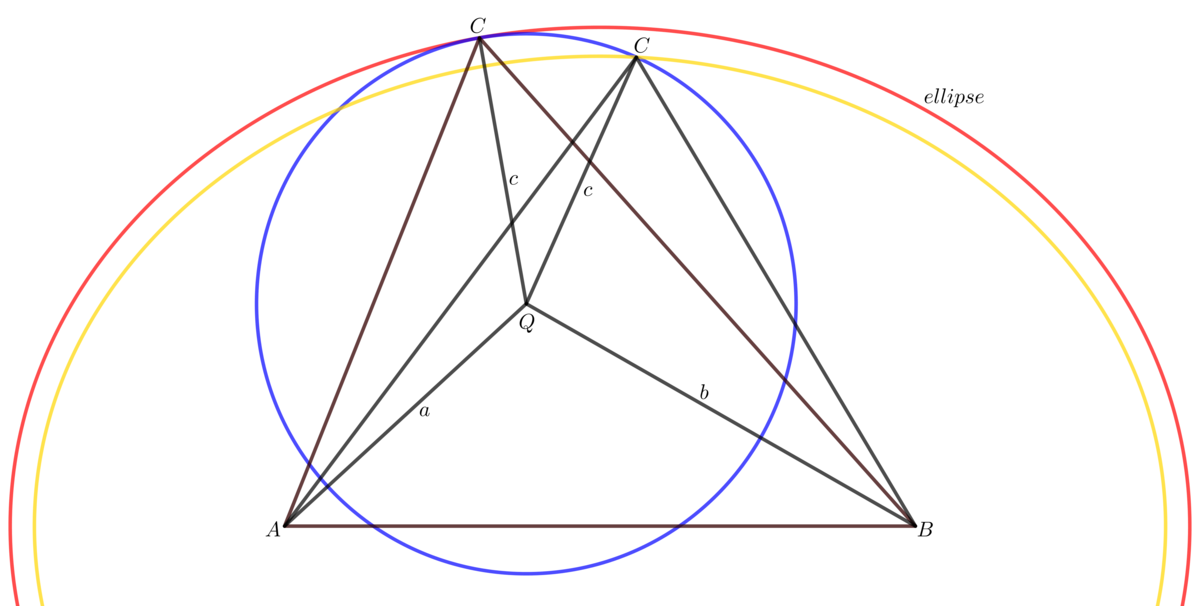 Let point C is on an ellipse with foci A and B, then AC+BC=major axis. From the drawing is clear, that for a fixed AB, a, b, and c, the maximum AC+BC is when the ellipse is tangent to the blue circle (Q, c), because the red ellipse has the biggest possible major axis. From the focus-to-focus reflection property => CQ is an angle bisector of an angle C. Analogically AB+AC is maximal when AQ is an angle bisector of an angle A and AB+BC is maximal when BQ is an angle bisector of an angle B => the largest possible perimeter is when
Q is the intersection point of the angle bisectors of ABC or Q is the center of the incircle of ABC.
Let point C is on an ellipse with foci A and B, then AC+BC=major axis. From the drawing is clear, that for a fixed AB, a, b, and c, the maximum AC+BC is when the ellipse is tangent to the blue circle (Q, c), because the red ellipse has the biggest possible major axis. From the focus-to-focus reflection property => CQ is an angle bisector of an angle C. Analogically AB+AC is maximal when AQ is an angle bisector of an angle A and AB+BC is maximal when BQ is an angle bisector of an angle B => the largest possible perimeter is when
Q is the intersection point of the angle bisectors of ABC or Q is the center of the incircle of ABC.
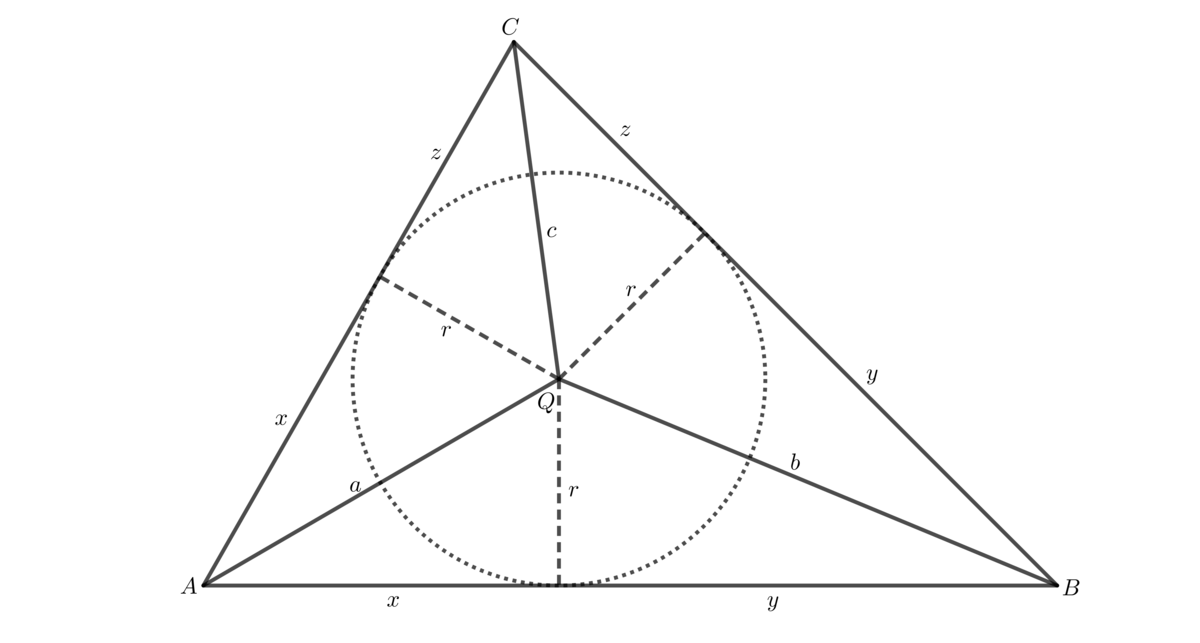 From the Heron's formula =>
A
A
B
C
=
2
p
r
=
2
p
x
y
z
2
p
=
x
+
y
+
z
x
2
+
r
2
=
a
2
y
2
+
r
2
=
b
2
z
2
+
r
2
=
c
2
If a=3, b=4, c=5 and solving numerically for p
⇒
p
=
2
0
.
9
3
2
3
3
0
3
6
7
9
6
9
3
3
7
9
5
8
2
0
2
0
5
2
6
⇒
2
0
9
3
2
From the Heron's formula =>
A
A
B
C
=
2
p
r
=
2
p
x
y
z
2
p
=
x
+
y
+
z
x
2
+
r
2
=
a
2
y
2
+
r
2
=
b
2
z
2
+
r
2
=
c
2
If a=3, b=4, c=5 and solving numerically for p
⇒
p
=
2
0
.
9
3
2
3
3
0
3
6
7
9
6
9
3
3
7
9
5
8
2
0
2
0
5
2
6
⇒
2
0
9
3
2
Log in to reply
Wow, nice approach - you might want to post it as a solution rather than a comment, though (so more people see it)
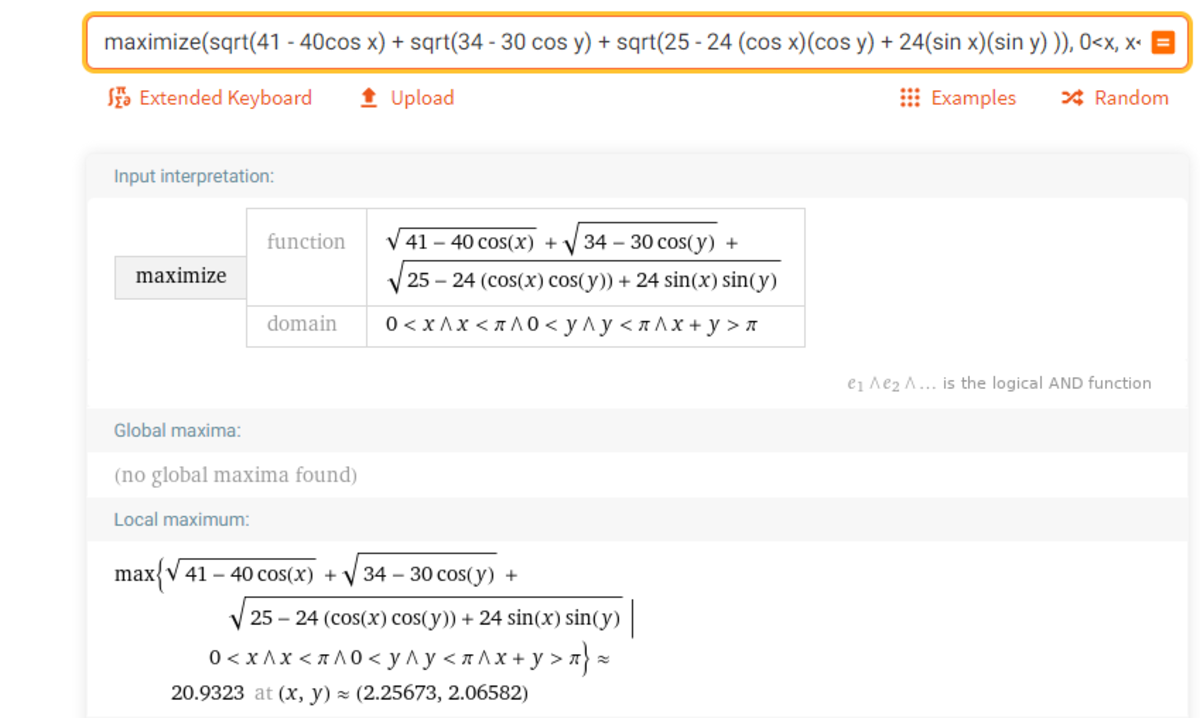
I generally don't post code for these types of problems, but Chris egged me on. :)
here is a picture of the triangle.