Yet Another Power Tower
a a a ⋅ ⋅ ⋅ = 3 1
How many positive real solutions a does the above equation have?
Hint : Argue "from first principles", without using any properties of the infinite power tower you might know.
Clarification : The value of the infinite power tower a a a . . . is defined as the limit of the sequence x 1 = a , x n + 1 = a x n , if that limit exists.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Summarized this means a limit for the power tower exists only for the fixpoint a (=value of tower) if and only if ∣ f ′ ( a ) ∣ < 1 with f ( x ) = a a x . (You proofed clearly what I assumed in an earlier posting.)
This only happens in the valid interval [ 1/e, e ] for a. In all other cases the tower converges against at least 2 limits or perhaps not a bit.
Log in to reply
The condition turns out to be "if and only if ∣ f ′ ( a ) ∣ ≤ 1 ". The two "Grenzfälle" need to be examined separately... we have done the case a = e earlier. Also, my work above does not prove that the sequence converges when ∣ f ′ ( a ) ∣ < 1 ; one needs to check that the seed x 1 = a 1 / a is in the "basin of attraction". The condition ∣ f ′ ( a ) ∣ < 1 guarantees convergence only locally .
"This only happens in the valid interval [ 1/e, e ] for a. In all other cases the tower converges against at least 2 limits or perhaps not a bit." There is a third possibility: If a > e then the power tower of a 1 / a converges to a value other than a , as in this case ; it converges to the value b < e such that a b = b a . If 0 < a < e 1 , then the power tower of a 1 / a approaches a two-cycle, as our collaborative solution here shows.
If you could explain what the (c,c) value refers to, I could try graphing the trajectory
Log in to reply
Thanks for the offer! The figure would involve the graph of y = ( 2 7 1 ) x and the line y = x , for 0 ≤ x ≤ 1 ; they intersect at the equilibrium point ( c , c ) = ( 1 / 3 , 1 / 3 ) . Then it would be fantastic if you could draw a cobweb starting close to 1/3, maybe at 0.3 or 0.31 or 0.32... you would have to experiment a bit and see what looks best. Hopefully, we would see a limiting two-cycle emerge between circa x = 0 . 0 8 and x = 0 . 7 7 , with the cobweb approaching the corresponding rectangle.
If we start a cobweb at our initial point 1/27, it should approach the limiting cycle from the outside, that is, x n will be more than 0.77 or less than 0.08, in an alternating fashion.
Clearly, many people are having a hard time with these nested problems. (As of right now, this problem has 277 attempts and 56 solvers.) Some people just find the equilibrium point in the hope that it will be the solution. I trust that a good figure will go a long way in explaining things.
Thanks again!
Log in to reply
Can you explain what the term conweb refers to?
I think you mean something like this :
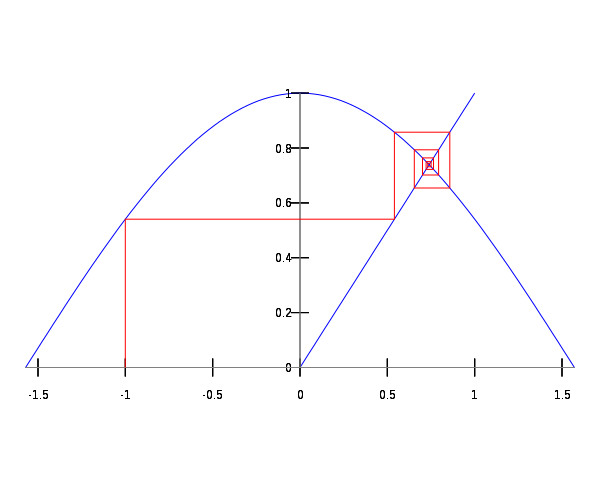
But I do not know what this is either
Log in to reply
@Agnishom Chattopadhyay – Yes, that's a cobweb indeed! In a technical sense, you do this: Starting with any point a on the x -axis in the domain of a function f ( x ) , draw a vertical line segment to the graph, then a horizontal line segment to the line y = x , then a vertical to the graph again etc. This is a way to visualize the sequence x 0 = a , x n + 1 = f ( x n ) .
Log in to reply
Interactive Version , with variable starting points.
Does this do the job?
Log in to reply
@Agnishom Chattopadhyay – Wow, this is fantastic! Thank you so very much!
Log in to reply
@Otto Bretscher – No problem. I had fun doing this
Log in to reply
@Agnishom Chattopadhyay – I don't know how much time this takes... if it's quick, could you perhaps do one of those here ? It would be tremendously useful!
Log in to reply
@Otto Bretscher – I posted a comment in the solution to the problem
1/3 is outside the domain [ 1/e, e ] valid for power towers!
True; you are invoking a powerful result due to Euler. But can you prove "from first principles" that 3 1 fails to be in the range, without using Euler's result?
A lot of people naïvely "solve" these nested problems without worrying about convergence, just finding a fixed point of the iteration (as of right now, this problem was 64 attempts and 17 solvers). They might come to the mistaken conclusion that a = ( 3 1 ) 3 is the solution. Convince them that this isn't the answer!
Log in to reply
Why should it be in the domain [1/e,e]?
In the moment I can not fix the problem exactly. But I strongly guess it has something to do with the first deviation at the fix point of the function y = a a 1 x . It has value -1 for a=1/e and is less than -1 for a=1/3 but greater than -1 for possible values a<=e where deviation reaches 1.
With the help of a little VB-application one can show that there are two limits for the tower, namely 0.078 and 0.77.
Log in to reply
Indeed, the problem is analogous to this , with a = 2 7 1 instead of a = 0 . 0 5 .
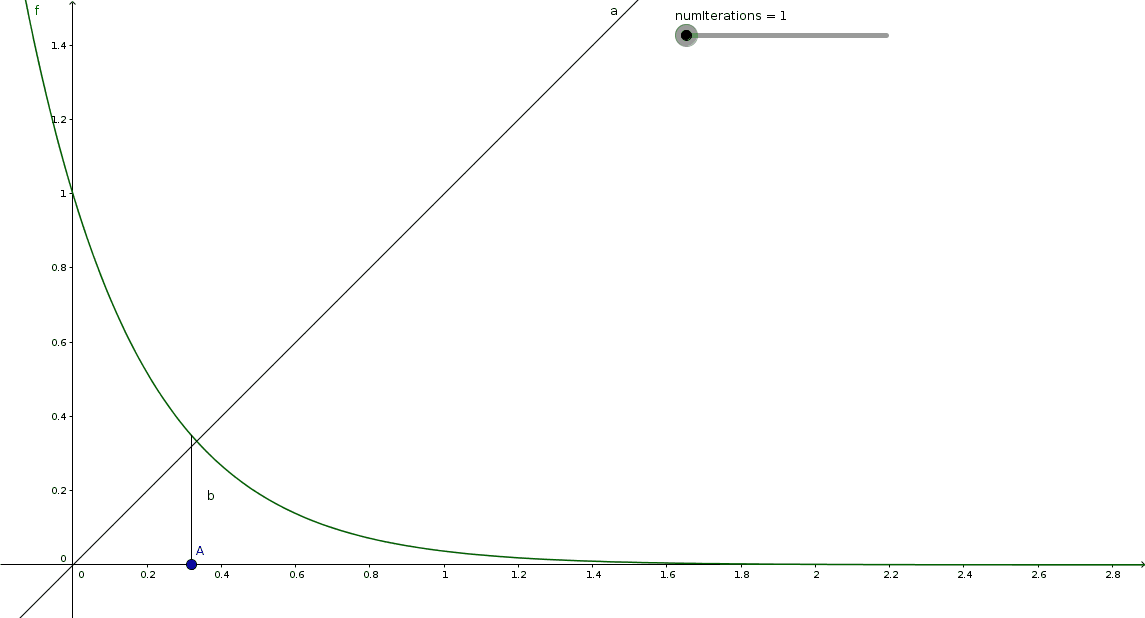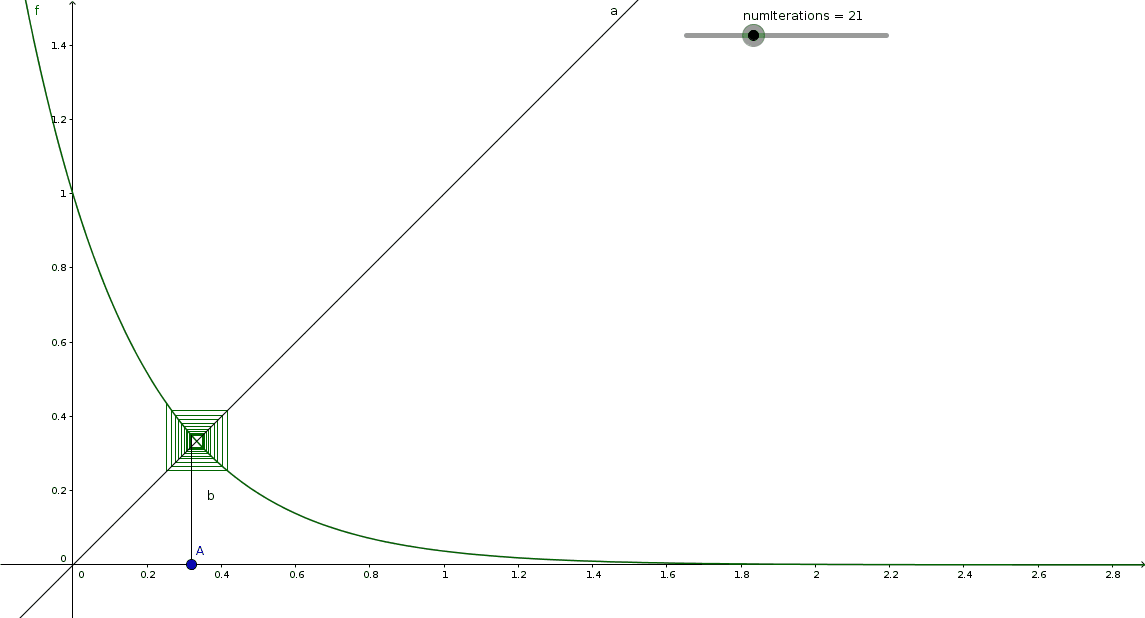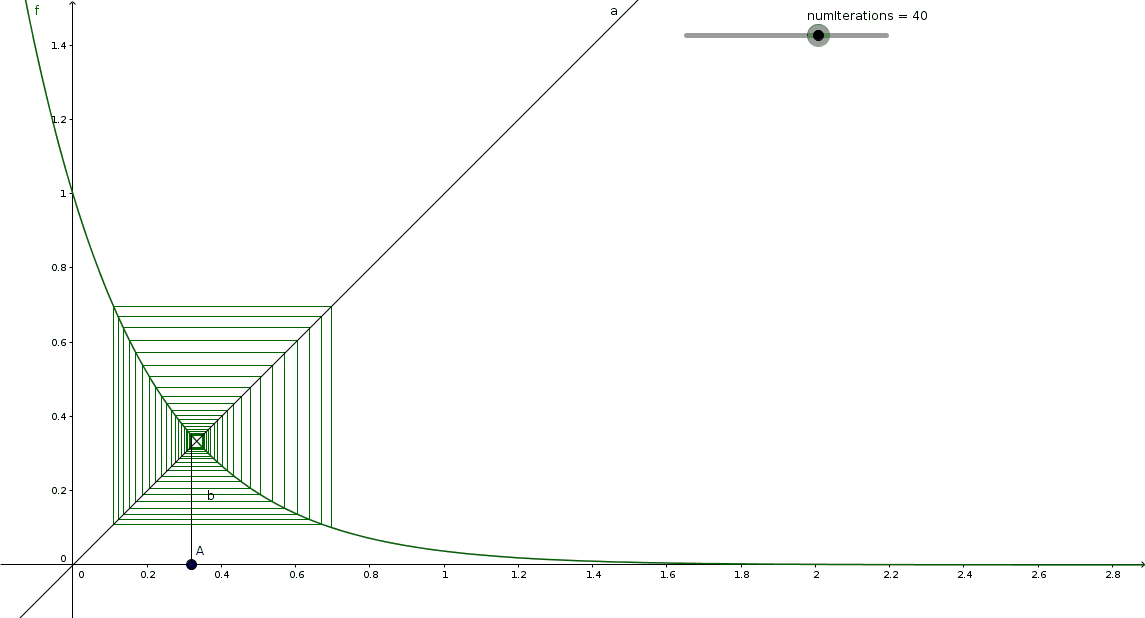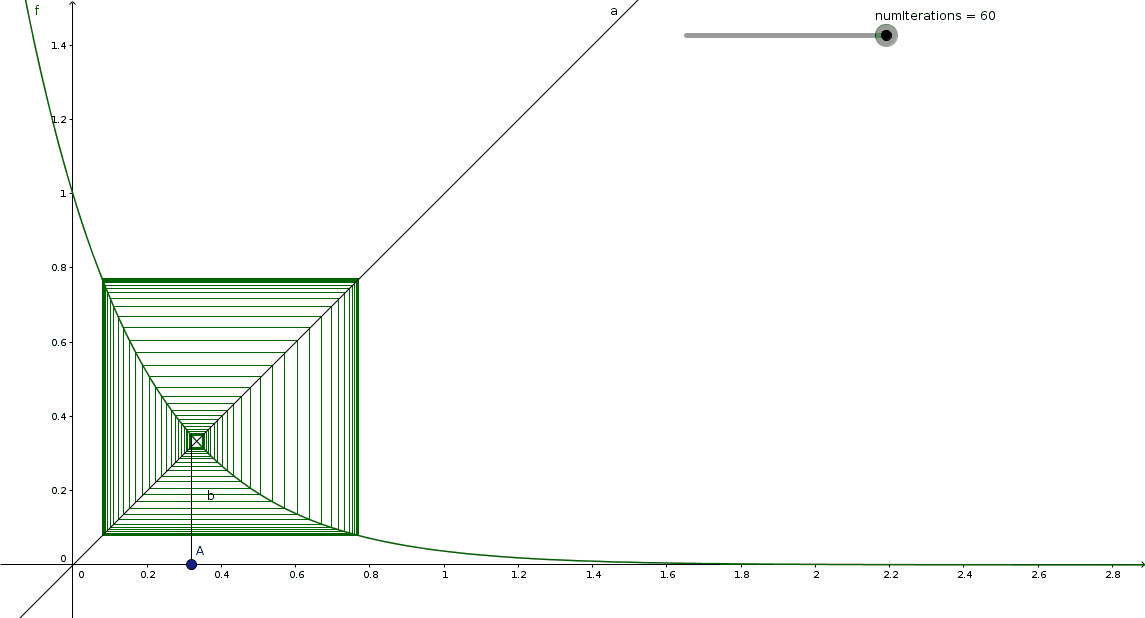
My solution will summarize the discussion we had with @Brian Charlesworth , @Andreas Wendler et alii. See Andreas' solution.
If we had a solution a , then the equation a 1 / 3 = 3 1 would hold, so a = ( 3 1 ) 3 = 2 7 1 . This shows that the given equation has at most one solution. The value a = 2 7 1 may or may not be a solution, and there cannot be any other solutions. We need to examine whether the sequence x n associated with a = 2 7 1 actually converges to c = 3 1 .
If we define the iteration function f ( x ) = a x = ( 2 7 1 ) x , then we observe that f ′ ( x ) = ln ( a ) a x so f ′ ( c ) = ln ( a ) a c = ln ( a ) c = − ln ( 3 ) < − 1 . This implies, by the Mean Value Theorem, that x n fails to converge to c . Indeed, if x n is sufficiently close to c (but not equal to c ), then ∣ x n + 1 − c ∣ = ∣ f ( x n ) − f ( c ) ∣ = ∣ f ′ ( p ) ∣ ∣ x n − c ∣ > ∣ x n − c ∣ , for some point p between c and x n : The equilibrium point c actually "repels" x n .
If you draw a cobweb starting sufficiently close to c , it will "spiral away" from the point ( c , c ) , at least initially. (I wish somebody could produce a graph illustrating this behaviour; I'm not good at this.)
Thus the given equation has no solutions.
PS: This discussion applies to any c < e 1 .