Heating water
A conical container of height 1 m , inner radius 2 m and outer radius 3 m contains water which is held at 1 0 ° C . The temperature outside the container is 8 0 ° C . If the thermal conductivity of the container is 0 . 5 W / m ° K , find the rate of heat transfer. Give your answer in watts ( W ).
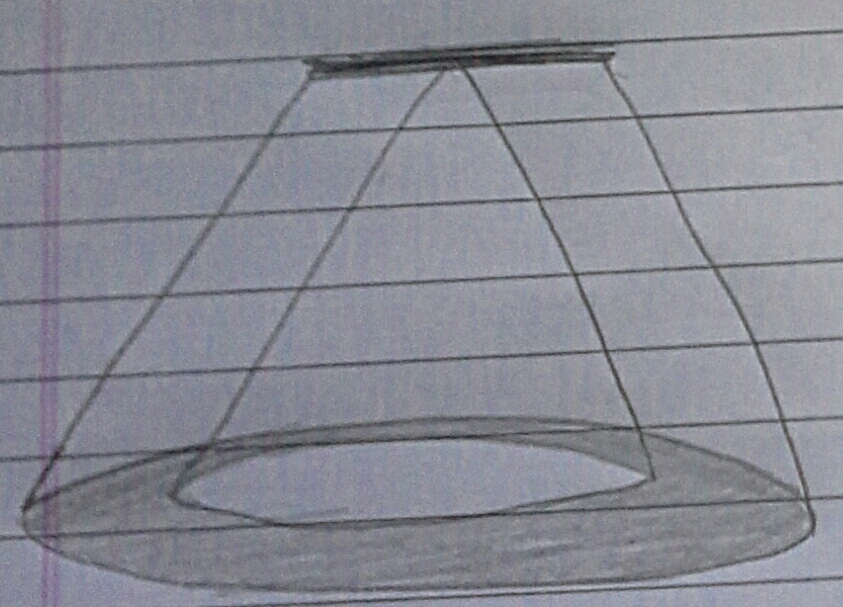
Assumptions and Details
- Assume that the base is thermally insulated and thus no heat passes through the bottom.
- The conical tip of the container is cut in such a way that the inner cone's tip coincides with the upper ceiling of the container which is thermally insulated.
The answer is 715.105.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Do you change your answer if it is wrong?
Log in to reply
We cant change our answer once the question is posted. It can only be done by the staff.
Log in to reply
You missed some points in your answer. The hight h is related to x and it is not constant. This will change all the equation you resolved.
Log in to reply
@N S – No, the cone is completely filled so, height is not related to x. Height swould have been related if the cone was half-filled or sort of. But since it is fully filled and the base is thermally insulated, the heat flows only through its curved surface area. I had kept that point in mind while posting the question. For clarity, I specified "completely filled" in my question now.
Log in to reply
@Ashish Menon – When you take the small strip the hight will not be constant.
I will not argue if you don't see about what I am talking
Log in to reply
@N S – Oh dont take it that harsh. I see you mean that height would be cinstant because if some extra negligible height which gets added in the top at its peak. Hmm, I neglected it cuz in a 3 m wide strip it wont cause much differnce, but yeah its still a fact. I've added that assumption in to assume the height constant throughout. Thanks!
Log in to reply
@Ashish Menon – OK.. let me try to explain it in other words
When you integrate the conical strip you start from inside to outside. The inner cone has a smaller hight and smaller curved side area. Going to the outer cone the hight will increase with x increasing.
Log in to reply
Log in to reply
@N S – The pic i put was misleading sorry for that, I've removed it. I'll put the one above now. Thanl Ks!
Log in to reply
@Ashish Menon – OK. This solves the problem of hight but the area of the curved side will not stay as you wrote it.
Now you must consider the truncated cone side surface.
Later after you do the correction and finish about the maths of the problem we can talk about the phisics of it if you want.
Very interesting problem. Must be level 5.
Log in to reply
@N S – Do you mean the curved surface area? So hopefully the final answer is correct now. I've done the correction. Thanks for the compliment yes we can talk about its physics.
Log in to reply
@Ashish Menon – Now let's talk phisics
The path of heat conducted through the cone must be the shortest. In our case it is perpendicular to the surface
It is logic, the thickness of the cone is not 1m. It's 1/sqt (10)
Log in to reply
@N S – Oh my, thats true!
@N S – Yes, this means that the heat does not travel radially outward. (This question was inspired from a similar question but a cylindrica one). I tried on a cone but yes, since there is a constant decrease in the radius, the heat flow would not be radially outward. Oops, I didnt consider that in my solution, my bad. After correcting all the errors which you might specify further I would post the new version of this question.
Log in to reply
@Ashish Menon – Yes, I think you can work this question again and put it in a new version. Thanks for the good job you do. Frankly, I waited to see the answer of this question because it is very interesting especially if you keep the original photo where it was a real container. One last thing, try to chose the dimensions in the new version of the question as real as possible. In real life you don't find a container of hight 1m and radius 3m.
Once more, thanks and keep on your nice work.
Log in to reply
Log in to reply
@N S – No worries, I would tag you as soon as its done. My exams get over in three days or so. I would work on it asap. Ah, I see you are interested in seeing how it would turn out in real practice. Normally, factories boil water to upto very hot steam or so to generate enough kinetic energy for turbine rotation. But I am not aware of the temperatures.
@N S – Thanks to you. Hmm what are the dimensions used in real life though?
@N S – Do you mran 5 1 .
@N S – Wait do you mean i should consider the truncated surface i just cut but that is thermally insulated.
@N S – Ah its getting more complicated, we should even cut off the top region, the curved surface area is not as it is now. I see what you mean.
@N S
–
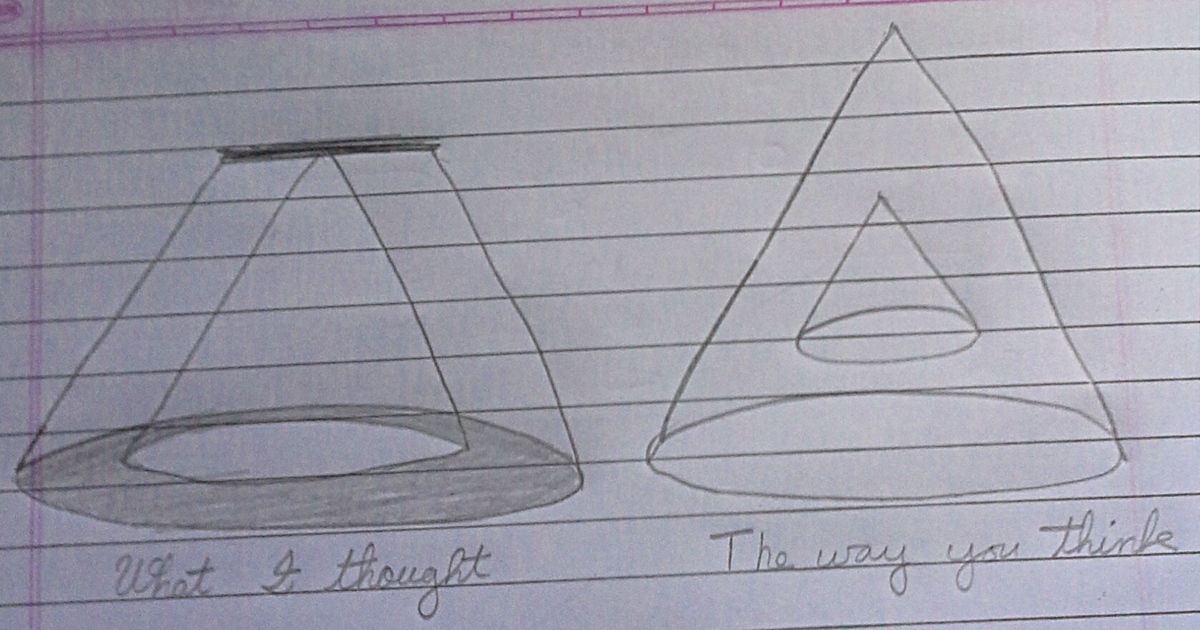
Ah I see that my problem is poorly phrased, look the pic below. Thanks for pointing out that, I'll fix it in a bit.
please physically explain how ( x 2 + h 2 ) changes WRT x??
The answer I am getting is 709.42 . The question accepted this value . If you all agree with my answer , I shall publish a report .
Taking a frustrum of bottom radius r , you will get the surface are through which heat is emitted as
A = 2 π ( 1 − r ) 5
The process to calculate this goes as -
Imagine complete cone , with upper imaginary conical part to complete cone .
Let the angle which the botom makes with cone's inclination be θ .
t a n θ = 0 . 5
S = c o s θ π r 2 − c o s θ π ( r − 2 ) 2
Radius of upper imaginary part of cone can be calculated easily by trigonometry.
Now using
P o w e r = d r K A Δ T
Answer comes as P = l n 2 7 0 π 5
Consider a small conical strip in the material of the container of width d x such that the temperature difference between its ends be d θ .
Applying the formula, t Q = l k A ( T 1 − T 2 ) .
t Q x h 2 + x 2 1 d x ∫ r 1 r 2 x h 2 + x 2 1 d x [ h ln ( x ) − ln ( h ( h 2 + x 2 + h ) ) ] r 1 r 2 h ln ( r 1 ( h 2 + r 2 2 + h ) r 2 ( h 2 + r 1 2 + h ) ) t Q = d x k ( π x x 2 + h 2 ) d θ = Q k π t d θ = ∫ T 1 T 2 Q k π t d θ = [ Q k π t θ ] T 1 T 2 = Q k π t ( T 2 − T 1 ) = ln ( r 1 ( h 2 + r 2 2 + h ) r 2 ( h 2 + r 1 2 + h ) ) k π h ( T 2 − T 1 )
Substituting the values, we get:-
t Q = ln ( 2 ( 1 2 + 3 2 + 1 ) 3 ( 1 2 + 2 2 + 1 ) ) 0 . 5 × π × 1 × ( 8 0 − 1 0 ) = 7 1 5 . 1 0 5