You can guess but can you prove it?
Identical circles, 1 , 2 , 3 , tangent to each other, are tangent to inner circle 4 .
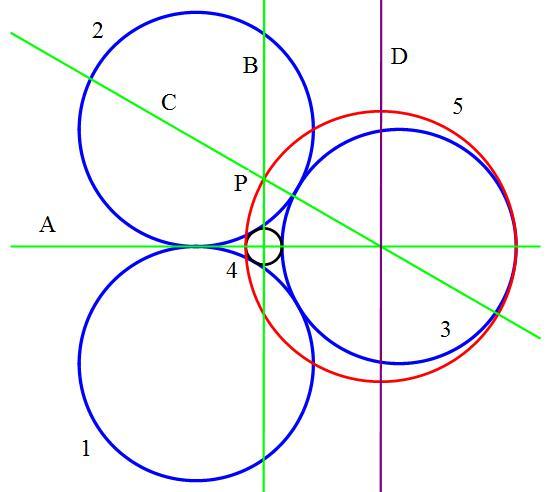
Circle 5 is tangent to circles 3 , 4 inside it. Line A passes through the centers of circles 3 , 4 , 5 . Line B , perpendicular to Line A , passes through the center of circle 4 , and intersects circle 5 at point P . Line C passes through point P and the center of circle 5 .
Find the small angle between lines A and C in degrees.
Note: Line C does not pass through the centers of circles 2 and 3 !
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If you form a triangle with lines joining the centers of circles you get an equilateral triangle , the line A bisects it so the angle is 30(in degrees)
YEAH I UNDERSTOOD THANKS A LOT
Prahkhar, I'm sure a lot of people know that the centers of circles 1 , 2 , 3 form an equilateral triangle, and conclude that the green lines form a 3 0 degree angle. But it's not the same thing, and it's a bit trickier to prove the latter. I think this is one of those problems where most people guess at the correct answer by jumping into a conclusion for the wrong reasons.
OH well, thanks , can you please put up the solution to this problem
Log in to reply
Hey, you know, I'm looking through my notes on this, and I don't have any proof of this at all! I'm hoping someone will come and offer a clear proof! It must be true, because so many people have said it's 30 degrees!
Log in to reply
I'm not too sure, but I think I got a somewhat nice one. It's just an application of the Pythagorean theorem and similar circles properties.
Edit: it gets pretty ugly but I think there's a way to skip the ugly steps, but I don't know how to skip them.
Actually, i just realized that I wasted a lot of time writing a proof when it actually comes down to this congruency between the blue and red triangles.
 this one congruency
this one congruency
Log in to reply
@Trevor Arashiro – Wow, I really have to squint at your Euclidean method of proof. I've found it peculiar that this seemingly "obvious" geometry should be so messy to try to prove by classical means. Sometimes direct algebraic analysis is much quicker, which can be done as follows
Let r be the radius of circle 4 . Then we know that
1 2 + ( 2 1 ( r + 1 ) ) 2 = ( r + 1 ) 2
From this we have r = 3 − 3 + 2 3
Then, using the geometrical mean theorem, we can find the height from the center of circle 4 to point P , which is r ( r + 2 ) , and so we work out that
2 r ( r + 2 ) = ( r + 1 )
proving that the angle is indeed 3 0 degrees
Log in to reply
@Michael Mendrin – Very true, it's much harder to prove through more algebraic methods. However, in my original proof, I found individual segment lengths and proved the congruency from there using
cos − 1 ( C 5 P C 5 C 4 ) ⇒ cos − 1 ( R 5 R 3 )
c o s − 1 ⎝ ⎜ ⎜ ⎛ 3 1 0 3 5 ⎠ ⎟ ⎟ ⎞ ⇒ cos − 1 ( 2 3 ) = cos 3 0
Note C 5 C 4 = R 3 . Also, C n = circle center n
Here are the congruences (A is the point of intersection of circles 3 and 1):
A C 3 = C 4 C 5
C 4 A = C 4 P
C 4 C 3 = C 5 P
Log in to reply
@Trevor Arashiro – Let me think of a way to simplify your Euclidean approach, using your ideas.
hey, Trevor, can you please make this proof a bit more clear thanks.
Log in to reply
What I did was find the individual lengths of each side of the two triangles P C 4 C 5 and C 3 C 4 A . Then I used cos − 1 ( h y p o t e n u s e a d j a c e n t ) to find the angle that we are looking for. But more specifically, what part do you need me to make more clear. I'd be more than happy to do so
let line A meet point of contact of circle 3 and 5 be C join the points of intersection of B with 3 and 1 to C and simplify [try coping the image to paint and try to edit as mentioned above]
Get your smaller blue circle's radius as a factor of bigger blue's. (How?) Construct an eq. tri joining big blue's center. Orthocenter, incenter, etc etc all co-incide. Recall that median is split up in 2:1. Hence, Some arial geometry will give you the relation. Then focus on the triangle P - (Center of small blue's) - (Center of Red's). Some obvious trigo and voila!