You complete me
× □ 1 0 9 9 1 □ □ □ □ 1 1 □ 0 □ 9 6 9 0 8 0 0 8 7 □ 1 □ □ □ 9 1 1
Above shows an incomplete long multiplication. What is the maximum number of digits I can still remove to allow only one unique solution?
Details and Assumptions :
- For example, I can remove one of the number "1" in the very last column and I'm still able to find the unique solution. So I can remove at least more digit to allow one unique solution.
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Is there a specific reason why you chose two prime numbers? What if they are both composite numbers instead? Can we remove more or less digits?
I think we can remove the 1 in the second line.
Log in to reply
Then 1 9 7 9 × 9 0 9 = 1 7 8 9 1 1 is also another solution which makes the solution not unique.
Log in to reply
This solution doesn't fit the format of problem. We will have a line with five squares instead of four squares.
Log in to reply
@Abdelhamid Saadi – Then the first square has a number 0.
Log in to reply
@Pi Han Goh – What I mean is that for the solution 1 9 7 9 × 9 0 9 the fifth line will be 1 7 8 1 1 which need five squares instead of four squares.
Log in to reply
@Abdelhamid Saadi – Oh, then take 1 9 7 9 × 5 0 9 .
First i would say that you have added 1 extra block in last(answer) line, between 9 and 6..
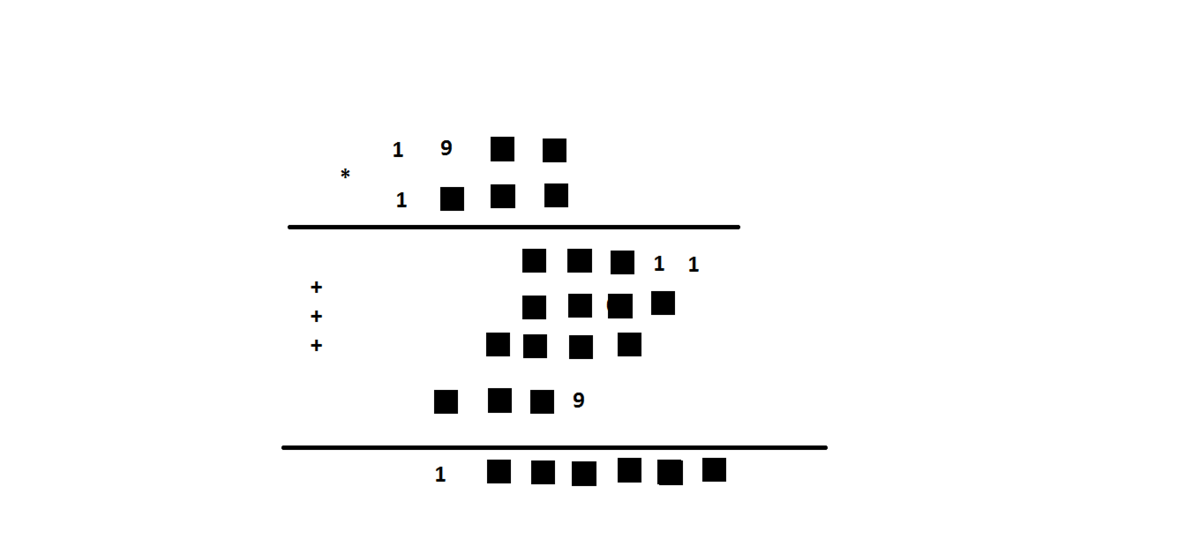
How do you frame such questions??
Then what is the very last box suppose to be?
Log in to reply
I didn't got you..i meant to say that answer will have 7 digits..and in the problem it seems to have 8 digits..
Log in to reply
Oh, okay edited. But what is the very last box suppose to be?
Log in to reply
@Pi Han Goh – Answer 1996811
Log in to reply
@Charlz Charlizard – No. I could have 1039 * 1103 = 1146017 which fits your long multiplication as well, so your answer is not unique.
Log in to reply
@Pi Han Goh – Yeah..you are correct..i have edited the solution...
Log in to reply
@Charlz Charlizard – Oh okay, your solution looks very similar to mine, you could move the 3 digits in the middle rows to the top and bottom rows to make it similar. But you need to explain why 14 is the maximum.
Let Y and Z denote the values of box in the first row and the box in the second row respectively. Beucase the last digit of 9 Y is 1, then Y has to be 9 only. And if Z is any integer larger than 0, then the product is greater or equals to 1 9 7 9 × 1 0 1 9 > 2 0 0 0 0 0 0 which contradicts the fact the leading digit of their multiplcation is 1.
So the original multiplication is 1 9 7 9 × 1 0 0 9 = 1 9 9 8 6 1 1 .
It's easy to verify that both 1 9 7 9 and 1 0 0 9 are prime numbers so we could not modify the digits in the first two rows. Thus we can remove all the digits in the third to sixth row:
× □ 1 □ □ 9 □ □ □ □ □ 1 1 □ □ □ □ 6 9 0 □ □ □ 8 7 □ □ □ □ □ 9 □ 1
And because we must keep of the last digit and the first digit of the product, we can remove all the other digits the very last row.
× □ 1 □ □ □ □ □ □ □ □ 1 1 □ □ □ □ □ 9 0 □ □ □ □ 7 □ □ □ □ □ 9 □ 1
However, we can still improve on reducing the digits given by noting that 1 9 7 9 × ( 1 0 0 9 + W ) > 2 × 1 0 6 if W > 0 , so we still can remove the zero in the second row.
× □ 1 □ □ □ □ □ □ □ □ 1 1 □ □ □ □ □ 9 □ □ □ □ □ 7 □ □ □ □ □ 9 □ 1
We shouldn't remove any of the 1 's in the first two rows else we can see that there is multiple solutions.
And if we remove any of 9 or 7 in the very first row, there wouldn't be a unique solution, just take 1 9 6 9 × 1 0 0 9 as an example. Hence we have removed the maximum number of digits, which is 14.