You wanted a Staircase Problem Trevor?

Geometry Level 4

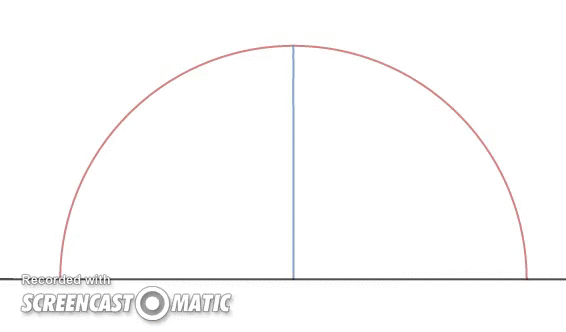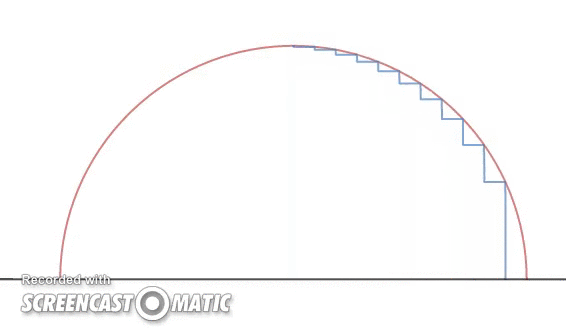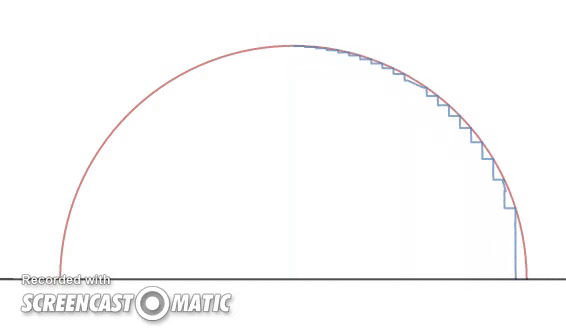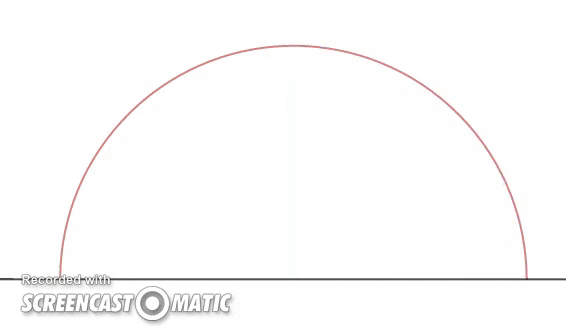Trevor is at the edge and inside of a circular semicircle of radius 1. He walks a distance of $d$ towards the radius of the semicircle and climbs up until his head hits the top of the semicircle. Then he walks another distance of $d$ maintaining the same height as when he hit his head the first time and climbs up again until his head hits the semicircle. This continues like a staircase pattern and when he reaches the top, he stops and shouts in victory. (The GIF shows an illustration of it)

Let $d=\frac{1}{n}$ where $n$ is an integer more than 0 and $D_{n}$ be the total staircase-zigzag distance traveled by Trevor.

Find

$\lim _{ n\rightarrow \infty }{ D_{n} }$

Assume Trevor has a height of $0$

4

\frac{\pi}{4}

\sqrt{2}

2

2 solutions

Brian Charlesworth
May 11, 2015

Edit: For sake of clarity I've interpreted this question as Trevor making $n$ horizontal steps of length $\dfrac{1}{n}$ and then determining $\lim_{n \rightarrow \infty} D_{n}.$

No matter what positive integer $n$ is, Trevor will end up making $n$ steps of length $\dfrac{1}{n}$ to the left, (assuming that he starts at the right edge), and $n$ steps up that have an aggregate length of $1.$

So $D_{n} = 2$ for any positive integer $n$ , and thus $\lim_{n \rightarrow \infty} D_{n} = \boxed{2}.$

@Julian Poon Fun question, but I think that you meant for the leftward steps to each be of length $\dfrac{1}{n}$ for a positive integer $n.$ (Otherwise the final limit doesn't really make sense.)

Brian Charlesworth - 6 years, 1 month ago

as the number of steps increases will it not approximate the circumference of the circle ...... why does it not converge to $\frac{\pi}{4}$

Abhinav Raichur - 6 years, 1 month ago

So we have a curve that's tending towards the shape of another curve. (Let's call this other curve the "limit curve.")

Even if a curve tends towards a limit curve, its perimeter doesn't necessarily have to tend towards the perimeter of the limit curve!

Now you're probably thinking, "Does this mean that Riemann sums don't work? It's basically the same thing but with area." Well, this doesn't happen with area!

The main difference is this. If a shape $A$ contains a shape $B$ , we know that the area of $A$ is definitely larger than the area of $B$ . In symbols: $(A\supseteq B)\implies(\operatorname{area}(A)\ge\operatorname{area}(B))$ However , this is not true for perimeter — If a shape $A$ contains a shape $B$ , the perimeter of $A$ is not necessarily larger than that of $B$ ! For example, $A$ might be a circle, while $B$ might be a shape with a really wiggly and complicated boundary. In symbols: $(A\supseteq B)\nRightarrow(\operatorname{perimeter}(A)\ge\operatorname{perimeter}(B))$

Why does this matter? Well, think of a Riemann sum. We have an upper Riemann sum and a lower Riemann sum. Because the upper Riemann sum contains our shape, and our shape contains the lower Riemann sum, the upper and lower sums respectively give us an upper bound and a lower bound on our area. So we know that the area of our curve must be between the these upper and lower sums. It's sandwiched between these two sums. So we get to use something like the Squeeze Theorem (aka Sandwich Theorem) to show that the area of our curve is equal to the limits of the Riemann sums. (This only works if the upper and lower Riemann sums have the same limit, but they have to be if our function is Riemann integrable.)

But when we try to do the same thing with perimeters, we find that the perimeter of the zig-zag curve doesn't really tell us anything about the perimeter of the circle. (So we don't get any upper bounds or lower bounds on our perimeter.)

P.S. Note that if $A$ and $B$ are convex , and if $A$ contains $B$ , then $A$ must have a larger perimeter. Try drawing (or imagining) some shapes to convince yourself of this. That's why this thing works.

Akiva Weinberger - 6 years, 1 month ago

@Akiva Weinberger – @Akiva Weinberger thanks for writing up in detail .... i get the difference now :)

Abhinav Raichur - 6 years, 1 month ago

It's the same flaw in this question .

Pi Han Goh - 6 years, 1 month ago

@Pi Han Goh – wow :) got trolled :p ...... then does it mean that the riemann sum we use for integration is flawed ?? .... else what is the difference between this and the riemann approximation for area under curve?

Abhinav Raichur - 6 years, 1 month ago

@Abhinav Raichur – The flaw is that we are still considering the perimeter of "zig zag" lines, when in fact a circle don't have "zig zag" edges. Read up Pythagoras Paradox.

Pi Han Goh - 6 years, 1 month ago

Yeah, i realised that a few hours ago... sorry...

Julian Poon - 6 years, 1 month ago

Can you update the problem phrasing accordingly? It is still not clearly phrased.

Calvin Lin Staff - 6 years, 1 month ago

@Calvin Lin – I've edited it. Mind if you have a second look?

Julian Poon - 6 years, 1 month ago

@Julian Poon – Unfortunately, I have absolutely no idea what you are trying to say.

It still says that "he walks a distance of $n$ ". So for $n \geq 3$ , don't we have $D_n \geq 3$ ?

Like Brian said, should it be "He walks a distance of $\frac{1}{n}$ "?

Also, what's this about "Trevor hits his head"? Are you assuming that Trevor has a height of 0? If he has a height of > 1, then the would never walk. If he has a non-zero height, he would not be touching the edge of the dome.

Calvin Lin Staff - 6 years, 1 month ago

@Calvin Lin – I've added that Trevor's height is $0$ as well as that n is smaller or equal to 1

Julian Poon - 6 years, 1 month ago

@Julian Poon – Haha. Poor Trevor; he's just a particle now. :)

I think the key here is that Trevor always makes an integral number of steps towards the center of the circle, and I don't think that specifying that $n \le 1$ will necessarily accomplish that. If, for example, $n = 0.4,$ then after $3$ steps "towards" the center, (and two moves up), he'll have overshot the top of the circle. My sense is that the easiest way to address Calvin's concerns at this point is to adopt the wording I used in my solution. This ensures that an integral number of steps are made, and most closely matches the visual concept of the problem that your gif demonstrates.

Brian Charlesworth - 6 years, 1 month ago

@Calvin Lin – I also want to change the GIF into a clearer one but I can't change it. This is the clearer one:

Julian Poon - 6 years, 1 month ago

@Julian Poon – I have updated the gif accordingly.

Unfortunately, talking about Trevor (even as a particle) climbing this "circular dome" still raises up some issues. Is the dome solid? If so, how does he walk? If no, how does he climb? The dome aspect also makes me want to think of this as a 3-D problem, and my initial thought was that he was walking on the inside/outside of the surface, where taking the "horizontal" steps meant in the x-y plane on the surface, and the "vertical" steps meant in the z-direction. In that way, i didn't understand the GIF.

I now understand this problem better, and I think that the phrasing could be improved upon.

Calvin Lin Staff - 6 years, 1 month ago

This topic of $\pi=4$ is described here .

Very nice problem btw. It's unlike any of the others.

Trevor Arashiro - 6 years ago

@Trevor Arashiro – @Trevor Arashiro thanks:)

Abhinav Raichur - 6 years ago

Akiva Weinberger
May 13, 2015

The horizontal segments have a total length of $1$ (imagine them each sliding down towards the $x$ axis). The vertical segments have a total length of $1$ (imagine them sliding towards the $y$ axis). Thus, the total is $2$ .

You wanted a Staircase Problem Trevor?

2 solutions

0 pending reports