You will like this problem
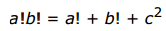Given that
a
,
b
, and
c
are positive integers, solve the following equation.
What is the least value of
a
+
b
+
c
?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
This solution is incorrect as it makes a leap of logic by requiring that { a ! − 1 , b ! − 1 } = { 1 , c 2 + 1 } .
Why a! - 1 = 1?
Log in to reply
@Linh Tran I used the fact that a ! − 1 is a positive integer and c 2 + 1 has imaginary roots, so it can't be factorized in ( a ! − 1 ) ( b ! − 1 ) until one of them is equal to 1 and other is equal to c 2 + 1 .
I like the approach that you used, to simplify the equation by factoring it nicely.
However, as Linh pointed out, you made a leap of logic by requiring that { a ! − 1 , b ! − 1 } = { 1 , c 2 + 1 } .
Log in to reply
@Calvin Lin I used the fact that a ! − 1 is a positive integer and c 2 + 1 has imaginary roots, so it can't be factorized in ( a ! − 1 ) ( b ! − 1 ) until one of them is equal to 1 and other is equal to c 2 + 1 . Please point out if something's wrong.
Log in to reply
It can't be factorised in terms of c.But that does not mean it is not factorable over all c. For example, c = 5 gives c 2 + 1 = 2 6 = 2 ∗ 1 3
Log in to reply
@Siddhartha Srivastava – Oh! Silly me. Then I think bashing is the way.
i did not understand how you did a !-1=1 and also the subsequent solution
Guessed it !
given equation can be written as
1 = 1/a! + 1/b! + c*c/(a!b!)
Now it is clear that sum of three positive real numbers is 1
and also a >=1, b>=1. As we know factorial starts form 0 but a and b cant be zero.
Also we can conclude that values of a and b cannot large.
By giving simple guess u will find that a and b have to be 2,3 or 3,2.
hence c=2.
at last 3+2+2=7 or 2+3+2=7
Given that, a ! b ! = a ! + b ! + c 2 ,
a ! b ! − a ! − b ! = c 2
Add 1 to both sides,
a ! b ! − a ! − b ! + 1 = c 2 + 1
a ! ( b ! − 1 ) − ( b ! − 1 ) = c 2 + 1
( a ! − 1 ) ( b ! − 1 ) = c 2 + 1
Here comes the guessing part, as a!-1 is not equal to 0, then put
a ! − 1 = 1
So, a = 2
And, b ! − 2 = c 2
Clearly, b ! = 6 Therefore b = 3 And c = 2
So, a + b + c = 7