You're gonna love this!
The positive reals x , y and z satisfy the given equations:
x 2 + x y + 3 y 2 = 2 5
z 2 + 3 y 2 = 9
z 2 + z x + x 2 = 1 6
Find the value of ( x y + 2 y z + 3 x z ) 2 .
The answer is 1728.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I skipped every tedious yet simple calculations such as cos 1 5 0 ∘ = − 2 3 to make the solution clearer. However, you should try it your own to completely understand the solution.
There are many problems that uses this skill, that is visualizing the system of equations into a geometric object. If there is a demand, I think I can write a wiki about it, but I'm not sure how to name it.
Log in to reply
Really very Nice Question I enjoyed in solving it !! And Actually I learn This Technique from this Question of you @Christopher Boo
No Calculus allowed and i really suggest you to make wiki about this So that everyone student of our Community can learn this Concept !! And I think You may be use the Title * Algebrometric Equations * for this wiki !!
And You may add this for examples in wiki Like this Not very difficult
Did the same way.
Nice solution. In completely unrelated news, 1728 is 1 2 3 .
Log in to reply
Even more, 1728 is 1729 minus 1.
Log in to reply
Which is the first taxicab number.
1 7 2 9 = 1 2 3 + 1 3 = 1 0 3 + 9 3
Taking the cancelling power 3 function, we have
1 2 + 1 = 1 0 + 9
1 3 = 1 9
3 = − 3
Half life 3 confirmed.
Furthermore, a triangle has 3 sides
Illuminati confirmed.
I can't see the image can anyone provide it to me pls.
Wow, good job! :)
This is an amazing solution! Never saw this way of solving a system of equations. Brilliant!
Isn't this very old problem?. I remember a similar problem on brilliant, which became very famous. The question was like this, x 2 + x y + y 2 = 9 , y 2 + y z + z 2 = 1 6 , x 2 + z 2 + x z = 2 5
Log in to reply
This problem appears in Arthur Engel "Problem solving Strategies"
If I remember correctly, that was easy because the equations are similar. When I was solving this, I am not sure if the area formula can lead me to the beautiful ( x y + 2 y z + 3 z x ) 2 .
Log in to reply
I wanna upvote it a million times. @Christopher Boo Thanks for such a great solution. BTW Can I find similar problems somewhere else? I need to practice this great method. Thanks again!
Log in to reply
@Satvik Golechha – You're welcome. Here are some problems I found that used this similar trick. You'll know when to use them when they have 9 , 1 6 , 2 5 or it looks like a distance formula.
I suppose this is the triangle that is missing in Christopher's solution. (At least it is the one I used to obtain mine in the same way as he did.)
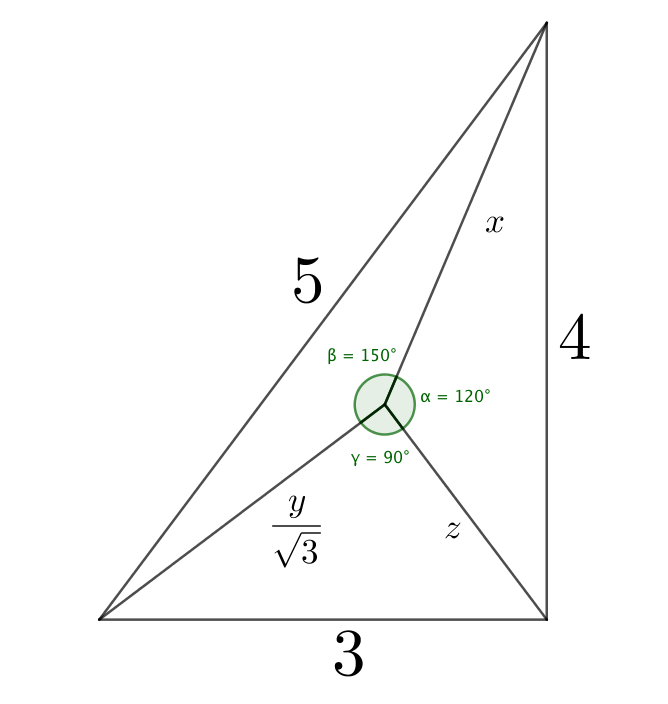
You get the desired result by adding up the areas of the three triangles as explained by Christopher. Check his solution for the details.
First, take a look at this triangle:
By Cosine Theorem,
a 2 + b 2 − 2 a b cos C = c 2
The triangle is carefully constructed to have the following lines:
A B : z 2 + 3 y 2 = 9
B C : z 2 + z x + x 2 = 1 6
A C : x 2 + x y + 3 y 2 = 2 5
The area of triangle is given by
[ A B C ] = 2 1 a b sin C
[ A B D ] + [ B C D ] + [ C A D ] = [ A B C ]
4 3 x y + 2 3 y z + 4 z x 3 = 6
x y + 2 y z + 3 z x = 2 4 3
( x y + 2 y z + 3 z x ) 2 = 1 7 2 8