Is 0.9999 ... = 1?
True or False?
0 . 9 9 9 9 … = 1
Note:
The "
…
" indicates that there are infinitely many 9's.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
60 solutions
Discussions for this problem are now closed
Moderator note:
Simple standard approach.
Another approach would be to use the Infinite Geometric Progression Sum . We have
1 0 9 + 1 0 2 9 + 1 0 3 9 + 1 0 4 9 + … = 1 − r a = 1 − 1 0 1 1 0 9 = 1
The part where you subtracted the equations. That is where you are wrong. The unending trail of 9s cantbe cancelled by another trail. That is just not defined because it repeats infinitely.
do you believe 1/3 = 0.333333333........ if yes then multiply both sides by 3 you would get (1/3)x3 = 3x 0.33333333........ => 1= 0.9999999999.......
1/3 does not equal .33333333. That is a lazy approximation.
@Chad Sedam – What? 1 divided by 3 is 0.3 recurring.
You are confusing the number of digits of a representation of a number to be the number itself. The digits of π are also infinite. Does that mean 1 0 π − π is not defined?
This is why I think it can be cancelled:
now, instead of thinking of an infinite number of 9 's, we see it as two 9 's:
x 2 = 0 . 9 9 ... , 9 x 2 = 1 0 x 2 − x 2 = 8 . 9 1
Now, we think of n 9 's:
9 x n = 9 − 9 × 1 0 n = 9 − θ
As you can see, as n approaches infinity, θ approaches 0 . So as n approaches infinity, which is what is happening here, it becomes valid to subtract.
Your argument has a flaw. The above is defined despite repeating indefinitely. It is, however, wrong to sum 2 diverging sums.
As for your "quotation" of Wikipedia, your argument still remains vague and has not, in my opinion, enabled me to understand your point better. How does it question calculus? And what has your "every possible thing happening around the world for a particular topic" got anything to do with whether an infinite sum exist?
Here is why I fell they are not equal.. Equal means exactly equal..and even though the difference is very very less, we cant say them to be equal until they are the exact same figures. To illustrate..
0.00000........infinite times....1 = 0 ??
No..
Also infinite*above no. is indefinite but infinite *0 = 0.
So no matter how less the diff.. is we CANNOT say they are equal unless they actually are.
@Hitesh Nankani – "0.00000........infinite times....1 = 0 ?? "
Yes. What you need to realize is that because it is infinite number of zeros, we never get to the place to write down the 1. Ever. And therefore it is precisely 0. Not almost zero, not "tending to" zero, "close enough to be called". Exactly zero. If you always try to think about it in terms of a series of finite approximations which are "really big", you will always miss the key point... we never get to the 1. Ever.
Your argument is incorrect, the trails can be cancelled, and it is a valid operation, although the recurring part is infinitely long. See this .
Yeah I read the article. Wikipedia refers to every possible thing happening around the world for a particular topic. With all due respect, sometimes it cannot be true. Think of it yourself, if the unending trail could be cancelled, then all the work of Newton and Leibnitz is rendered useless regarding calculus. So what I believe is 0.9999... tends to 1.
@Abhishek Dass – It never "tends" to 1, it is 1. If we have a long, but finite string 0.99999.....99, then I accept that it "tends" to 1. Because the string is infinitely long, it is equal to 1. Well, I see that my argument has mathematical rigor. If you think that 0.9999....... ad infinitum tends to 1, prove it yourself. By the way, @Abhishek Dass , I see that you (or we) are nowhere at a stage to question the validity of information provided on Wikipedia. The fact that 0.99999....... = 1 is an important result used in Bayes's Calculus too, and hence you cannot say that this result is a contradiction to work on Calculus.
@Venkata Karthik Bandaru – its tend to be 1 but not equal to 1. for above, we have this notation in Maths ≈, means 0.99999 ≈ 1 . this is true .
@Muhammad Ahmed – I agree with Muhammed Ahmed, this is an approximation that approaches 1, but that doesn't mean it ever actually reaches 1. It may get infinitesimally close, but unless it can reach 1, it is not 1; it's approximately 1 "means 0.99999 ≈ 1 . this is true ."
@Muhammad Ahmed – Yes, you are correct that it tends to 1 but not equal. It seems a practical solution for those who believe it equals one would be write out 9.9999...until they reach 1 then reply back to let us know they found 1.
@Jerry Wirth – It's basically the same as limit of n -> infinity of 1/n, we will never at which point it will equate to 0, but we do know it equals zero in some shape or form.
@Muhammad Ahmed – Im Looking for this!
@Muhammad Ahmed – No it equals one.
@Andrew Wilson – if its equal to one then why we need limits and approximation in maths, then no use of this sign " ≈". tell me why we use this????????????????????
@Muhammad Ahmed – Because 0 . 9 9 9 9 9 is not the same as 0 . 9
0 . 9 has a repetend, and every number that can be represented with a repetend is a rational number. The repetend of 0 . 9 9 9 9 9 is 0 , while the repetend of 0 . 9 is 9
The rational number that 0 . 9 represents is 1 . It just so happened that the number 1 can also be represented as 0 . 9 , though this representation is less popular because it's less simpler to write.
I may have been the only one to notice this, but there is a reason why 1 can be represented in two ways in Hindu–Arabic numeral system. In decimal notation, if all the digits to the left of the decimal point are 0 , the absolute value of the real number being represented doesn't get less than the absolute value of it raised to a positive integer. On the other hand, if not all of the digits to the left of the decimal point are 0 , the absolute value of the real number being represented doesn't get greater than the absolute value of it raised to a positive integer. 1 neither gets less nor greater than 1 raised to a positive integer, which is why it can be represented either way. This is also true even in binary, octal, etc. Just an observation on mathematical notation.
1 − 0 . 9 9 9 9 9 = 0 . 0 0 0 0 1 ≈ 0 1 − 0 . 9 = 0 . 0 = 0
0 . 9 9 9 9 9 ≈ 1 , but 0 . 9 = 1 .
@Muhammad Ahmed – It's not an approximation. It equals 1. It is an infinite number of 9s
@Andrew Wilson – If I have 1 spec of dust in the universe - lets say its a white spec, and the resy of the universe is black. i.e 0.999999999999999999.....% of all the matter in the universe. Does the spec of dust not exist? Lets make the spec of dust the size of a planet. Does that not exist either.....lets make it the size of a galaxy....again? does that not exist? Youre a complete buffoon mate.
@Andrew Wilson – So when exactly does it stop being 1 and become something else? At what point EXACTLY does it not become 1. You're a complete idiot.
@Karl Walker – Your mistake is that you are thinking of it as a progression of numbers of finite length, looking for the "point" at which it "becomes" the infinite progression. But a finite representation never "becomes" the infinite progression. If you approach it in this fallacious manner, then it will always seem confusing. The important thing is to recognize that the infinite number of 9's is fundamentally different than any finite number of 9's. It is either an infinite number of 9's or it isn't. If it isn't, then it is less than 1. If it is, it is equal to one. Exactly.
There are any number of references and demonstrations that can easily be found online by qualified individuals which will support this conclusion. You don't have to take anyone's word for it here.
Here's a good one for those without much training in mathematics:
http://www.purplemath.com/modules/howcan1.htm
@Karl Walker – 0.999... IS exactly 1. It doesn't stop becoming 1. It IS 1.
The "..." is important. It's not a fixed number of 9s, it's infinite.
If they are not the same, you should be able to tell me by precisely how much they differ. Not an approximation, not a "tends to", but an exact number.
So by how much, precisely, do they differ?
@Karl Walker – Wow, found the best idiot on brilliant, it is you sir !
@Andrew Wilson – In reply to Andrew. Erm.....No it doesnt. I dont know where you learned to do mathematics mate, but 1=1 Try writing 0.99999....... In binary. It certainly is not 1
@Karl Walker – 0.999... is just another way of writing 1. Just as one is another way of wring 1. Just as 1.000000... is just another way of writing 1.
They are the same thing.
@Venkata Karthik Bandaru – 0.9999..99. Does not tend to zero 0.9999....... Does Because tending 1 does not mean 1 but an infinitesimally small number less than 1, a number which can not be thought of For eg. If u take 0.999999999999999999999 Then also there exists another number which is even more closer to 1. So u cannot say that if it is finite then only it tends to 1. Apparently if it is non finite, then only we can say it tends to 1
@Pruthvi Patel – It is .0001 short of "1".Write a comment or ask a question...
@Venkata Karthik Bandaru – Wikipedia can be tampered with by anyone who thinks that they are right. The correct answer is that it does not. Simple if you know your stuff.
@Eddie Spollin – I agree with the above statement if it equals to 1 then why is it a completely different number? Infinite or not logic tells me that 0.999999… is not the same as 1 as you can see although in retrospect it still tends to be the same but still different example 1+2=3 whilst 0.9999999…+2=2.999999… and again this new number is similar actually almost the same but to say that it is exactly the same is undoubtedly false . Now try multiplying them and look at what you get 1 2=2 but 0.999999... 2=1.9999999… so it is common for most people to say it is the same simply because it is easier and we are a naturally lazy species but say the numbers are the same goes against the value they both have there is nothing more to be said I hope you all understand this as I have tried to make it as simple as possible but still there are techinicalities which prevale against ;)
@Shehan Melanka – Do you agree 1/9 * 9 = 1 Do you agree 1/9 = 0.1111111...... Do you agree 0.1111111...... * 9 = 0.99999999..... 0.99999999...... = 1
@Shehan Melanka – If it were a finite stiring of 9s you'd be correct. It's not, it's infinite.
https://www.youtube.com/watch?v=G_gUE74YVos
@Shehan Melanka – In your argument, you have not yet proven that 0 . 9 9 9 9 9 9 . . . is a different number by saying that 2 . 9 9 9 9 9 . . . = 3 , since you are already assuming that 0 . 9 9 9 9 . . . = 1 .
@Shehan Melanka – It's not a different number. It's the same number written a different way. For example "3" = "30/10" = "27^-3" etc. These number are all "3" even though they are written differently.
@David Aronchick – SO you meant that 1=0.99...9 bcs 30/30 = 1 ?? So tell me how 30/30 = 0.99..9 ?
@Muhammad Dimas Hertanto – No, not because. He is simply showing how a particular value can have multiple different representations. 30/30 does equal 0.999... because 0.999 is another way to write 1. To see this, write down the decimal representation of 1/3, and then multiply both representations by 3.
@Shehan Melanka – It's not a completely different number. It is a different way of writing the same number.
Just like 3/3 and one both equal 1. The number 0,999... is just another way to write 1.
@Venkata Karthik Bandaru – If .9999999 = 1 because .9999999 tends to 1, then it could be said that 0.51 =1 because .51 tends to one. If you can say that, then every increment from .51 to 1.49 could be said to equal 1 because every number in that range tends to 1. An example. If you want to know what 75% of 1 is, you could not use the equation 0.75 x 1 because that would be equivalent to saying that .75 % is 1 x 1. So if you want to know how much 1 is, you can not use the number .99999 because that would only be a percentage of 1. Seems clear to me.
@Kenneth Drew – 0 . 9 9 9 9 9 9 9 = 1
It is 1 0 x 1 0 x − 1 that tends to 1 as x approaches ∞ , but because x never reaches ∞ , 1 0 x 1 0 x − 1 will always be less than 1 .
1 0 x 1 0 x − 1 = 0 . 9 9 9 9 9 9 9 at x = 7 .
However, 0 . 9 9 9 9 9 9 9 is not 0 . 9
0 . 9 = 1 0 x 1 0 x − 1 because x never reaches ∞ .
1 0 x 1 0 x − 1 tends to 0 . 9 as x approaches ∞ . It does not become 0 . 9 . It only tends to it.
In other words, lim x → ∞ ( 1 0 x 1 0 x − 1 ) = 0 . 9 , but we know that lim x → ∞ ( 1 0 x 1 0 x − 1 ) is also equal to 1 , because 1 0 x 1 0 x − 1 tends to 1 as x approaches ∞ .
0 . 9 has a repetend, and every number that can be represented with a repetend is a rational number. The repetend of 0 . 9 9 9 9 9 9 9 is 0 , while the repetend of 0 . 9 is 9
The rational number that 0 . 9 represents is 1 . It just so happened that the number 1 can also be represented as 0 . 9 , though this representation is less popular because it's less simpler to write.
I may have been the only one to notice this, but there is a reason why 1 can be represented in two ways in Hindu–Arabic numeral system. In decimal notation, if all the digits to the left of the decimal point are 0 , the absolute value of the real number being represented doesn't get less than the absolute value of it raised to a positive integer. On the other hand, if not all of the digits to the left of the decimal point are 0 , the absolute value of the real number being represented doesn't get greater than the absolute value of it raised to a positive integer. 1 neither gets less nor greater than 1 raised to a positive integer, which is why it can be represented either way. This is also true even in binary, octal, etc. Just an observation on mathematical notation.
1 − 0 . 9 9 9 9 9 9 9 = 0 . 0 0 0 0 0 0 1 1 − 0 . 9 = 0 . 0 = 0
0 . 9 9 9 9 9 9 9 < 1 , but 0 . 9 = 1 .
@Kenneth Drew – It's not 0.999999999 though. It's 0.999... The trailing dots are important. It means an infinite number of 9s.
@Venkata Karthik Bandaru – Equal?? really?? In class 12 we learn calculus. Read the above comment regarding it.
@Abhishek Dass – Tends to but does not equal
@Abhishek Dass – its like an unstoppable force meets an immovable object..
You can say that it tends to 1 or is equal to one but both answers are contradictory to some person's work or some theorem and both the answers support some other theorems.
@Abhishek Dass – I totally agree with you
@Abhishek Dass – Correct it is always tends to Zero But theoratical mathemetics let it proof 1 which is obviously not correct.
@Saurabh Chauhan – Mind if you elaborate on your "obviously not correct"? Maybe a proof without any flaws?
What you have said is that Infinite times x - infinite times x = 0 Hence infinity - infinity = 0 Which is wrong It is a known "not definable" quantity in calculus. 0.999... Tends to one , but is not one
@Rhett Dsouza – Well, I see that my argument has mathematical rigor. If you guys think that 0.9999....... ad infinitum tends to 1, prove it yourselves.
@Venkata Karthik Bandaru – No problem, see my point above
@Venkata Karthik Bandaru – Dear Karthik, you know, when we solve a physics problem for instance, we imagine the problem. We think, get the logic right. And in most cases we get the answer straight away. But what if one imagination power isn't strong enough? We use Maths. That's where maths work. It has errors. Many. But somehow it makes our problems easy. And the chances of making mistakes increase. So what I'm trying to say that instead of clinging to mathematical loopholes or things like that, ask yourself. Your heart will say, " Yess!! It really tends to 1 ". You see, maths only comes when you can't get the logic. Do not take me rude please.
@Abhishek Dass – https://www.khanacademy.org/math/recreational-math/vi-hart/infinity/v/9-999-reasons-that-999-1
See this
@Shailendra Patel – Shailendra, thank you so much for sharing this link. It was quite a breath-taking watch, but brilliant in exploring the problem from every angle. I teach basic numeracy (GCSE Foundation Tier) to adults, so this may be beyond many of them, but I am always looking for ways to stretch my more able learners.
@Shailendra Patel – best response yet. the greatest conflict I'm noticing in this thread is between a stubborn refusal to acknowledge the subjectivity of math on one side and the unawareness of the subjectivity of math on the other.
@Mountain Scott – Math is not subjective.
@Shailendra Patel – This really helped me understand. Thanks!
@Shailendra Patel – I strongly oppose your "fact" because each proof has its flaws or assumptions. Another video by the same channel as above, https://www.youtube.com/watch?v=wsOXvQn3JuE
@Aneesh Kejariwal – You realise that's satire, right?
@Aneesh Kejariwal – Yes, all proof has some flaw or assumption.
@Abhishek Dass – yeah, and using your heart, you fail at quantum mechanics. congrats.
btw, in physics, this kind of problem does not even appear, since physics is more about practicality, and hardly has anything to deal with "the exact value". For instance, π to the first 3 0 decimal places is far from enough to calculate the size of the observable universe to an extremely precise measure.
@Julian Poon – Yes, exactly ! Thanks for your valuable comments throughout Julian Poon :).
@Abhishek Dass – I see no further meaning in trying to explain to you bro.
@Abhishek Dass – .99999... simply equals 1. His proof was correct.
@Abhishek Dass – In physics, we look at the problem, conceptualize, solve, and then check the internet to see if we screwed up before handing it in. Do that last step and you will find that all qualified people who internet will disagree with you.
@Abhishek Dass – I agree with Abhishek. I f 0.99999999...... would be EQUAL to 1, then we would always write it as 1 itself. We just round it off and take it to be 1 for convenience. As Karthik said 'The fact that 0.99999....... = 1 is an important result used in Bayes's Calculus too, and hence you cannot say that this result is a contradiction to work on Calculus.' is just because you can't keep on calculating with an infinite series. So we CONSIDER it to be 1. I hope you would agree that 0.9999....... is less than 1. Now, a number less than another can't be equal to it, right?
@Samriddhi Singha Roy – Mind if you elaborate, how would 0 . 9 9 9 . . . be lesser than 1 ? Or if not, find a number between 0 . 9 9 9 9 9 . . . and 1
@Julian Poon – "Mind if you elaborate, how would .9999... be lesser than 1 ? Or if not, find a number between 0.9999... and 1." Beautifully asked.
@Julian Poon – So .9999... and .9999999.....8 are equal and so is .99......8 and .99...7 so .99...7 and .999... are equal ? wait what?
@Aneesh Kejariwal – No because 0.999... has an infinite number of 9s. 0.999...8 does not.
@Julian Poon – The thing about infinity is that there is no end. So, no matter how many 9s you add to the end of 0.9..., I can add another zero prior to the 1 at the end of 1 - 0.9... = 0.0...01 meaning the numbers are not equal.
@Samriddhi Singha Roy – No. 0.99999..... = 1. Equal.
@Adam Bryce – Actually better to think practically, rather theoretically. It's true that our brain can't count infinity, so definitely we have no way to confirm 0.999...=1, it always tends to 1. but in practical aspect think of a thing that you are gonna break it in its smallest part , you simply can't as the physical world has its limit of having the smallest part. there will exist a smallest finite part of size lets say (1 x 10 ^-50), so when you accumulate all those small 1 x 10 ^-50 part say 9 parts (an element of size x is broken in 9parts each of size 1 x 10 ^-50) you will get 9 x 10 ^-50 which will make a complete element that is 1(it's not a lazy approach but a practical approach). Here we can say 9 x 10 ^-50=1 for our assumed world.So the result of this question depends upon kind of world and space we are dealing with. And this result will vary accordingly. And this question actually is unique tool for exploring infinite question with all providing different results
@Samriddhi Singha Roy – That's exactly why you're never supposed to write 0.999999......
@Rishu Bagga – Actually better to think practically, rather theoretically. It's true that our brain can't count infinity, so definitely we have no way to confirm 0.999...=1, it always tends to 1. but in practical aspect think of a thing that you are gonna break it in its smallest part , you simply can't as the physical world has its limit of having the smallest part. there will exist a smallest finite part of size lets say (1 x 10 ^-50), so when you accumulate all those small 1 x 10 ^-50 part say 9 parts (an element of size x is broken in 9parts each of size 1 x 10 ^-50) you will get 9 x 10 ^-50 which will make a complete element that is 1(it's not a lazy approach but a practical approach). Here we can say 9 x 10 ^-50=1 for our assumed world.So the result of this question depends upon kind of world and space we are dealing with. And this result will vary accordingly. And this question actually is unique tool for exploring infinite question with all providing different results
@Venkata Karthik Bandaru – Ok, let's see..
0,999... + 0,0010 = 1,0009999... (9 ad infinitum)
1 + 0,0010 = 1,0010000 (zero ad infinitum)
You can use (as you did) many "math apery" to embellish a lie.
Sometimes I ask myself if math translates the world [and the cosmos] as the Pitagorics wanted or if it translates only itself.
I guess the second possibility is more plausible. A clue of that is the fact that we use π (pi) to measure the circles. We are not able to measure circles like we do with poligons.
@Ayran Michelin – Exactly! Math is abstract. It does not necessarily represents only what we can understand/represent in a physical way. Even the concept of infinity already messes with the mind of fresh undergraduates. But, for me, 0.9999... is clearly = 1.
@Rhett Dsouza – Yes it is incorrect to sum divergent series, which is what you said about infinity - infinity. However, what we are dealing here are convergent series, which your argument does not cover.
@Rhett Dsouza – It is 1. Try doing 1 - 0.999...
It's zero as there is no end to the 9s It's not some massive number of 9s it's infinite.
@Andrew Wilson – So a pair of infinitely sensitive scales with two weights each side. one of 1kg EXACTLY and one with 0.999999-Infinty Kg on the other side with an infinite time period to settle would actually balance exactly for infinty would they? Think you might find you are wrong mate!
@Karl Walker – A 0.999999... KG weight IS a 1 KG weight.
At your link it is said - However, these proofs are not rigorous as they don't include a careful analytic definition of 0.999...
I am 100% in agreement with you Abhishek
If I go 90% of the way to touching my finger to my nose, I don't touch my nose. I do that again I still don't touch my nose. I do it an infinite number of times and I infinitely never touch my nose. When does not touching my nose equal touching my nose. Never!
If you do it an infinite number of times, what distance, precisely, is your finger from your nose?
This has nothing to do with mathematics tho. Anyways, you are never actually touching your nose. The atoms never really touch themselves, so... And by the way, 0.9 is not equal 0.999... :D
divide 0.9999..... by 9 = 0.1111.... divide 1 by 9 = 0.1111..... therefore 1 = 0.9999...
A similar proof to James Munday's below
Yes, this is one of the many elegant proofs of this result.
then according to you, 0.9999.... divided by 8(or any other number) should also be equal to 1 divided by 8(or any other number)?
Isn't that rounding it off?Because it will always be 0.000...1 lesser than 1.
0.0000...1 is not a real number. Why? Well, think about the real numbers. Take any two, and you can find another one halfway between them. So take 0.00...1 and 0. What's halfway between them? Nothing. You could say 0.00...05, but that's 0.00...5. And that's larger than 0.00...1, five times larger. It simply doesn't work.
Isn't it an infinitesimal, though?
@Hugo Sales – There is no infinitesimal in the real numbers other than 0.
When did half a number became 5 times greater? your a decimal place off my friend. if you think its equal why are there no person who writes his age with a string of .99999999.......9?
@Aaron Michail Jesoro – You have an infinite number of zeros then a 1. Then the 1 at the end becomes a 05. Now you have an infinite plus one number of zeros then a 5. But when you add 1 to an infinite amount the infinite amount doesn't change. So you just have an infinite amount of zeros then a 5.
Nobody writes their age as .99999999........9 because:
a) That's too long. Does anyone write their age as 37.0000...? As 74/2?
b) That's 1 year old. 1 year olds don't write their ages.
c) You don't put a 9 at the end. That implies it's finite. It's just 0.99... if you write it that way.
d) That's too many significant figures.
@Alex Bean – Thats an american education at work. No wonder you wont get further than serving at Mcdonalds!!
@Aaron Michail Jesoro – "if you think its equal why are there no person who writes his age with a string of .99999999.......9?"
If you think 1+1 = 2, then why are there no people who write their age as a 1+1?
@Ian Myers – right, about that, why is it that people don't write 1 0 as a representation of 2 cause it is correct but in base 2 . And similarly, why is it that we don't write e as ∑ n = 0 ∞ n ! 1 ? Because it is tedious to write it that way! However, that does not mean that they are not equal
You can never put that 1 at the end of 0.000...1. That means it equals 0.
No, it is not rounding off, and the result is well established.
God to say that .999...=1 is to throw away the value of precision or the concept of infinity .999... is .9+.09+ .009+.0009.... to make that into 1+.0+.00+.000 is just defeating the point of the pattern of the number just like .89999999. does not equal .9 you are just rounding up at an infinitely like saying 1/2+1/2^x infinitely gets closer to 1 , .89 can get infinitely closer to 1 but adding infinitely closer points to one.
.999…=∑_(n=0)^∞▒〖1-(〖10〗^(-n))〗≠1
If that were true, tell me precisely the answer to this. Not some vague, infinitesimal.
1 - 0.999... = ?
This is troubling for two reasons ... first, using fundamental calculus, we know that choosing the exponent x to be real, and positive real numbers (if we want to avoid complex numbers, anyway), that
lim(x→+∞) of a^x is +∞ if a is > 1, 1 if a =1, and 0 if 0<a<1; and lim(x→−∞) of a^x is 0 if a>1, 1 if a=1, and +∞ if 0<a<1.
That is, the limit of any number that is not exactly 1 to an infinite exponent is either 0 or +∞. Therefore, lim(x→+∞) of .9999...^x is 0, and lim(x→−∞) of 0.9999...^x is +∞. These are properties of the number 0.9999... that are beyond discussion ... regardless of any algebraic relationship to the number 1. Therefore, while I can easily concede that the numbers are algebraically identical, they are not absolutely identical. So the question is (with all deference to Bill Clinton, who once asked "what the meaning of 'is' is"), "what the meaning of 'equal' equals."
Second, and more philosophically, physics provides us the Lorentz transformation (or Omega) of (1-v^2/c^2)^1/2 as the factor for observational differences in spacetime as an object approaches the speed of light. All of special relativity relies on the assumption that (v^2/c^2) can never equal 1. Thus, the number, defined by physics as the maximum for that factor is, indeed, and actually, 0.999... . Unless we are ready to rewrite special relativity, we better accept that 0.999... does not equal 1, and move on to the next Brilliant question ....
i.e. tends to 1 but never equals to 1. Perfect!
No it equals 1 precisely. The starting assumption is wrong. 0.999... does not belong to the set of real numbers.
Unless you can tell me precisely (the exact number) the answer to this:
1 - 0.999... = ?
If it was equal to 1 then it would be written as" 1" . Clearly a fallacy. It approach we 1 but it never is equal. In mathematics it has to be wrong.
Just the same way why 1 can be written as 1 . 0 0 0 0 0 0 . . . . Even if something is equal, there might be other ways of expressing it, even when limited to decimal notation. If you insist on your point, mind of you give a more detailed explanation of why 0 . 9 9 . . . = 1 ?
Ok, let's see..
0,999... + 0,0010 = 1,0009999... (9 ad infinitum)
1 + 0,0010 = 1,0010000 (zero ad infinitum)
You can use (as you did) many "math apery" to embellish a lie. Sometimes I ask myself if math translates the world [and the cosmos] as the Pitagorics wanted or if it translates only itself.
I guess the second possibility is more plausible. A clue of that is the fact that we use π (pi) to measure the circles. We are not able to measure circles like we do with poligons.
This solution is completely incorrect. If you plot the line on x y plane then you will find that the two line will never intersect. By taking value of x arbitrarily you cannot prove your equation
If 0.9999..... would equal to 1 you would write just 1 instead of 0.9999.......
According to your logic 0.9999....=1.0000....
Hilarious. The correct answer is yes, Karthik Venkata writes a cast-iron proof that the answer is yes. Other correct statements are made to prove the answer is yes. Yet STILL people will not accept the simple truth that it is equal to 1. So funny.
Let 1/9 = .111111111.....
Then x both sides by 9 then the value is = to 1
No, the second value is not 1, it is .9999...
No way can 0.9999 be equal to 1 and the proofs are fallacious. Approximation yes but mathematical exactness, No.
That's because we're not talking about 09999 = 1. We're talking about 0.9999... = 1. There's a huge difference.
From what I can obviously see 1 = 1 . 9 9 9 9 . . . . ( a d i n f i n i t u m ) = . 9 9 9 9 . . . . ( a d i n f i n i t u m ) . 9 9 9 9 . . . . ( a d i n f i n i t u m ) = 1 − 1 × 1 0 − ∞ And I needed no loophole math to prove it, it just makes sense.
If I was to debate the validity of your math proving .9999..... = 1. I would start at the 10x .9999.... = 9.9999..... If was was more of a math nerd I would theorize something about you never quite converging on 9.9999... but I don't care enough to debate it or think about it.
To all of you who are going to yell at me for being an idiot, whatever, I'm wrong, it's not that important.
PS: Don't use fractions to try to prove this. If you use a fraction you will undoubtedly use a number with an infinite number of decimals. What that infinite number of decimals means is that number will never be quite exactly equal/representative to that fraction, it will always be an infinitesimal amount off.
PPS: If I were to do a limit type thing on that number then I would agree it equals 1. But that limit type thing would do it based on the calculus principle that being infinitely close is the same thing to being equal. Which is exactly what I am disagreeing with now. I agree, it might as well be 1, but it is still not quite 1.
It IS 1. Infinitely close means the same as "is".
If you were talking about a huge number of 9's recurring I'd agree. But we're not, we're talking about an infinite amount.
@Calvin Lin The approach through Infinite geometric Progression sum is wrongly used in the Challenge Master note. If must be like this:
1 0 9 + 1 0 0 9 + 1 0 0 0 9 + … = 9 ( 1 0 1 + 1 0 2 1 + 1 0 3 1 … ) = 9 ( 1 − 1 0 1 1 0 1 ) = 9 ( 9 1 ) = 1
Yes, I too agree ! I didn't notice it XD !
Yeah, I was about to point that out.
Gosh.. how did so many people miss that (including me)... I guess we just turned off?
- 9(1/10 + 1/100 + 1/1000....)
- 9(1((.1-(.1^infinity))/(1-.1)))
- 9(1((.1-.000...1)/.9))
- 10(.099999999....)
- .9999999...
This doesn't make sense in the real world. 0.9999 is approximately 1, but no matter how many places after the decimal you care to add, it will always be less than 1. If you were in a spaceship heading to the moon but your course was only 99.9999 ...% correct, you'd probably die, or at the least you'd land somewhere off-target. Add a million 9s after the decimal to your course, then try to reach Proxima Centauri - you won't end up where you thought you would.
You are correct 0.9999 is approximately 1, and 1 - 0.9999 is 0.0001. They are clearly not the same number. However 0.9999........ (to infinity) is not approximately 1. It IS 1. There is no number between 1 and 0.99999...... therefore they are the same number. It's as simple as that. It does not tend towards 1, it is 1. The algebraic proof given at the top is just that, PROOF. You can't argue with solid proof. You may not like the answer, but that doesn't mean it's wrong.
"but no matter how many places after the decimal you care to add, it will always be less than 1"
Correct. But this is the fundamental misunderstanding. If you can identify a "how many", then it is not an infinite number. When it is in an infinite number, then there is no "how many", and the argument is irrelevant.
If there is no number 1 it can't be 1 it just keeps going on an.....
The most interesting part of this thread is the fact that younger individuals seems to have a better grasp of the "abstractality" of mathematics. (Most correct answers I've seen were from younger individuals (less than 20, not less or equal 20, but less than 20 years old).
The reason this is true is because it as been defined this way. There's nothing keeping you from saying they're not the same - they look very diferent to me :D Now, the problem with 0.(9) is it always breaks something; if you define 1 to be equal to 0.(9) you break the idea that any number can have only one decimal (or any other base) expansion, but if you were to say they do not equal each other, you'd break something slightly more important - algebra. BTW, it is said that they must be equal to each other since 1 - 0.(9) "equals" 0.(0)1 (aka 0.000...1) which is not a "real number"; no it is not, but it is an infinitesimal.
but the question is "is 0.99999 = 1 ? " obviously no. ;p
does 0.00000.....1 matters ?
if the question is : " How 0.999...=1 OR Proof 0.999...=1" then its solvable.
9.999... fingers (what ever it means) = 10 fingers
9.999..=10
0.999...=1
I may be wrong, but i just wants to know how can you multiply an never ending number with any other number, and then subtract thinking it is a finite number. If what you did is true then why is it that infinity minus infinity not equal to zero and undefined
I'll be looking forward to the email from BRILLIANT about getting my points because upon further review they determined my original answer was correct.
It is true that 0 . 9 9 9 … = 1 .
You will not be getting an email saying that this problem has its answer updated.
Then what do you have to say regarding 1^(infinity) and .9999...^(infinity) . Thanks.
Actually 1 is different of 0.999...
You can compare to 2 straight lines: one is 90º and the other is 89.999...º If they are close to each other, and would be equals, then they would never approach or move away from each other. But in this situation, they are not paralel. It will happen somehow.
You can compare to % values. If you got 0.0...1% of chances to get rich for eternity, you would fell hopeful for it. If you got 0% even a small fraction of you, wouldn't be hopeful at all...
however, I don't agree with the answer, even it doesn't changing at all.
It is not true! The only number that is one is one
@Jacy Henry – Correct. And some ways to write one is 37/37, 0.33+0.67, 100-99, and 0.999...
Simply it is not equal to one because it is different than one for every digit "n" in number "x" while n tends to infinity there is a number "e= n-value/10" e>0 such that 1=x+e
Well.. is 0.00000...0001 = 0 then??
Yes. If you miss off the 1 at the end. And you have to miss off the 1 at the end or it won't be an infinite amount of 0s.
Let's see ..... can someone tell me the value of x:
x=1-0.999999........
x=1-0.999999... x = 0
It can go on for infinity but there will always be an infinitely away .1... So cannot equal something where a piece is missing no matter how small. Way away it is so close but never quite there. Maths game like buy at 30 borrow 10 off three friends. Negotiate deal at 25 keep 2 and give 1 back to friends. You owe each 9 so 3 nines are 27 plus 2 you keep is 29. Where is the 1
"So cannot equal something where a piece is missing"
What piece is missing? Can you write down the quantity that's missing?
Ok, let's see..
0,999... + 0,0010 = 1,0009999... (9 ad infinitum)
1 + 0,0010 = 1,0010000 (zero ad infinitum)
You can use (as you did) many "math apery" to embellish a lie.
Sometimes I ask myself if math translates the world [and the cosmos] as the Pitagorics wanted or if it translates only itself.
I guess the second possibility is more plausible. A clue of that is the fact that we use π (pi) to measure the circles. We are not able to measure circles like we do with poligons.
or you could think of it like this. if you were to give each of your nine friends one piece of a cake, they would each have 1/9 of the original cake. Since 1/9 is equivalent to 0.1111111... if all of your friends returned the piece they took, you would have 9/9 or 0.999999... which simplifies to one.
If you stop the expansion of 9s at any finite point, the fraction you have (like .99999 = 99999/100000) is never equal to 1. But each time you add a 9, the margin error is smaller (with each 9, the error is actually ten times smaller).
That's "if you stop the expansion". But it doesn't stop.
To lessen some of the confusion in this conclusion, I suggest you introduce the following caveat to the beginning of the question (although I suppose it's a giveaway):
"According to the Archimedean property, ..."
Under this (our conventional) understanding of mathematics, .9 repeating indeed equals 1, but under a hyperreal numerical system it does not.
In other words, you ought to establish the premise before arguing the conclusion.
.999... is the absolute closest you can get to 1 without ever actually reaching it, however since the difference is infinately small it may as well be written as 1.
1=1 No matter the string. Imagine 1/x as x approaches 0. 1/0 does not exist. 0.99999 no matter how long is NOT 1. I do not agree with this argument at all.
That is correct for any finite number of 9's. For the infinite case, there is no "how long" anymore, so any thoughts about "how long" are irrelevant to the situation at hand. This seems to be a very common stumbling block.
find product of square root of(-2} and square root of (-5).
− 1 0
Incorrect notation in the master challenge solution.
Write a commen But still .0001 short of 1.
This is related to one fundamental theorem of Real Analysis " Bolzano–Weierstrass theorem" if stated in simple form is that " there are infinite real numbers between any two real numbers"
This is related to a fundamental theorem of Real Analysis " Bolzano–Weierstrass theorem" if stated simply " between any two real numbers there will be an infinite number of real numbers"
x = 0,9999... Then 10x = 9,9999.... This is where it goes wrong, imagine there is n numbers of 9 if you multiply it to 10 then after the comma it will left you n - 1 numbers of 9
Both the answers are correct depending upon from which point of view you approach the answer approximation or cold logic both mathematical. comment or ask a question...
And what about greatest integer function??? [0.999....]= 0 and [1]= 1 Hence they aren't equal.
I dont agree to ur proof at all because it works only when u multiply it with 10. It doesn't prove when u multiply it with any other number. It can be said that 0.99999... = 1 only when every number in number system can prove it according to ur logic.
The number is not 1 so how is it equal to 1? That's like saying 4.999999... is equal to 5 when it is not because it is not 5. Just because it almost is something, doesn't make it so. They are not the same number or quantity so they cannot be equal even if they are separated by the smallest of amounts. This makes absolutely no sense.
You're right, it is very much like saying 4.999... is equal to 5. Because they are both true statements. They are simply different notations for the same thing, just as 20/4 is 5 and sqrt(25) is 5, so is 4.999... also another way to write 5. If you doubt this, write 1/3 in decimal notation and multiply both quantities by 3.
Write a comment or ask a question... But still .0001 short of "1".
this is not one it is always approaching 1 thats like saying 9=10
What if God said "no", 'cuz 0.99999....... is rougly 1 just "close to 1" but not exactly 1.
Prove it. Or if not, don't use god as your source for support
This solution is wrong. The equations that you claim prove it is true, merely cancel out the margin that .9999999... is less than 1 by.
Seems like a trick question, not a serious one.
No... Maybe depending on application it's close enough but it's not equal.
Karthik Venkata is right. 0.999... = 1. Not approximately, not rounding, not tending towards... but precisely equal. If you disagree, you need higher level math course work to study. It's a proven mathematical statement. It's as proven as the square root of 2 is irrational.
yeah higher education tells us that 2-1= 0.99999....9. USA has 0.999999.....9 president as of now
@Aaron Michail Jesoro – Since 1/3 + 2/3 is the same as 0.333... + 0.666..., then the two statements are equivalent. Thus 1/3+2/3=0.333...+0.666... Add the terms on each side becomes 3/3=0.999... Hence 1=0.999...
@Nathan Hall – Very good -- this is yet another elegant proof, and thank you for posting!
0.999... is not 'nearly' 1.0 or 'tending to' 1.0; it is equal to 1.0.
@Nathan Hall – this is the 1st solution to this that has made sense. thank you. also, not looking for a long winded debate; but just because someone doesn't understand 1 problem doesnt mean they are uneducated or "need a higher level math course work" they just need a solution that makes things click...like yours did for me! Thanks for the simplified solution!
@Aaron Michail Jesoro – No, not 0.99999...9 presidents, but 0.9999... presidents.
@Aaron Michail Jesoro – We're not talking about 0.999999.....9. We're talking about 0.999999.... There is no ending 9.
I guess I do. Some sort of course that allows you to disregard logic. Methods for manipulating the matrix. Red pill or blue pill?
@Jeff Wallace – To deny logic is to deny 0.999...=1. Logic dictates that this is true.
Since 1/3 + 2/3 is the same as 0.333... + 0.666..., then the two statements are equivalent. Thus 1/3+2/3=0.333...+0.666... Add the terms on each side becomes 3/3=0.999... Hence 1=0.999...
DEPENDING on application? In any application in any example in the entire physical universe, it is the same. The only room for argument lies in the mathematical realm alone. We can not measure an infinitesimal difference in the real world. Because of this fact, and the fact that mathematics is useless in applications where it has no use, it makes no sense to adopt a model where the two represent immeasurably different values.
By the same logic 1=2. Just adjust your scale of numbering so that in comparison 1 is insignificant. \( \infty + 1 = \infty + 2 ) so 1 = 2. When written down they look different, but for any application in the entire physical universe it is the same.
@Jeff Wallace – It is indeed wrong to sum 2 divergent series, as reflected in your point. However, it is valid to sum 2 convergent series.
The right answer is, 0.9999.... is NEARLY equal to 1 but NOT EQUAL to 1. If it was EQUAL then there is no meaning for " = " operator its meaningless EQUAL is STRICTLY equal. Well okay so your saying 0.9999 = 1 ..Apply greatest integer function.. u get diff results.
If you substract 0.99999....99 from 1 you will have 0.000000000...001 that is different. From 0.
Actually not quite, because you got to the place where you wrote down 1, which means it was not an infinite number of zeros, which means it was not an infinite number of 9's. When you realize that in the infinite case you never (not after a really really long time, but ever!) get to write down the 1, you'll realize that it is in fact precisely zero.
The fundamental misunderstanding that throws everybody off here is that you can understand the properties of 0.999... by looking at "really long" approximations to it that terminate. When you consider the case where it doesn't terminate, the behavior changes in a very important way that you will never see by looking at successive finite approximations.
We're not talking about 0.99999....99, we're talking about 0.999...
what ever... you followed my idea...
@Francisco Gallego – Yes. I followed your idea, but it was wrong.
0.999... and 0.999...99 are fundamentally different numbers.
0.999...99 is not equal to 1. 0.999... is equal to 1.
This is false.
maybe 0.999999... ≈ (approximately equal to) 1. but 0.99999.. is never equal to 1.
There is no need to post 3 duplicates of the same comment. What I think is that 0 . 9 9 9 . . . = 1 , see my point above. If not, here's a challenge: Find a number between 0 . 9 9 9 9 . . . and 1 .
Simple flaw you missed.. x=0.9999 then 10x = 9.999 & not 9.9999.....!!!
You have ignored the approximations in your proofs. 0.999.... could be considered 1 for all practical reasons, or by the approximations that calculus offers, but DOES NOT EQUAL 1 with the laws of number theory or inifinity
No it's wrong. If x= .9999999 and so on then 10x= 9.999999 and so on. I mean one less 9 will be there in the answer and you can not get the subtraction result as 9. if x=.9999999 then 10x= 9.999999 and the difference is 8.9999991.
1 is equal to 1. .9999999999999999999999999999 is not one its .9999999999999999999999. question should be taken out.
.9999 is emphatically NOT equal to 1. Ask any geneticist. Sloppy math, and shouldn't be here.
Well in our world 0.9999 recurring is about the same as 1. However if you were travelling in space for a trillion miles then 1 trillion and 0.9999... trillion miles would be noticeably different.
No it wouldn't as there's an infinite amount of 9s in that number. It's the infinite part that matters.
Let's use a practical example.
If you travelled 1 trillion miles. How far away from 1 trillion miles would 0.999... of a trillion miles be from a trillion miles?
p.s. If you are right, you should be able to give me an exact number.
If we are using math, then yes. .9999 equals one. However, in science it does not
Its not equal, besides you honestly believe everything written in wikipedia. Anyone can edit that. If they are equal 1 -0.9999999.... Should not have an answer unforyunatey it does
the fact that Wikipedia can be edited by everyone is one of the driving reasons that it is typically correct
for me 0.9999.... can't be equal to one.. because even though how many 9 we put in end their is a missing .00000000....00001 that will make it equal to 1. having that computation above will give way to find the missing .00000000....00001 therefore tricking us by looking that they are really equal.
for me, this argument is like an asymptote (gets near but cant really meet 0) and parellel lines (doesnt meet each other.)
There is no missing 00000000....00001 as there is no ending 1 at all.
WTF. You don't need calculus or physics to prove that 1 is not equal to .9999..... My 6 year old son only used subtraction to prove it. 1-1=0, 1-.9999=.0001 and .0001 is definitely not equal to zero. Your calculator will show you that.
there are not 4 9's, there is infinitely many 9's
Calculators do not show the exact values, and here we are not talking about a finite number of 9 's, we are talking about an infinite number of 9 's.
I see the school system has failed you. Math don't work that way son.
No problem! But I see your arguments come without any evidence. Also, mind your language, it reflects bad on you.
I'd really like to know your idea of how maths work. By the way, are you really 3 0 ?
This is a discussion, if you have nothing constructive to contribute, don't.
Equal = Equal, that simple.
@Jacy Henry – I find it really hard to believe you are older than me. If you aim to convince me, do a better job at it.
This is bogus I don't know what kind of math you Indians learn but those are not equal.
Please be respectful of others. There is nothing wrong with the solution.
The easiest way to show this is:
9 8 + 9 1 ⇒ 9 9 ⇒ = 0 . 8 8 8 . . . + 0 . 1 1 1 . . . = 0 . 9 9 9 . . . 1 = 0 . 9 9 9 . . .
Another way is by induction:
9 1 = 0 . 1 1 1 . . . 9 8 = 0 . 8 8 8 . . . 9 2 = 0 . 2 2 2 . . . ⇒ 9 9 = 0 . 9 9 9 . . . 9 3 = 0 . 3 3 3 . . . ⇒ 1 = 0 . 9 9 9 . . . . . . . . .
Posted this in Facebook some time ago, but I thought they are not equal
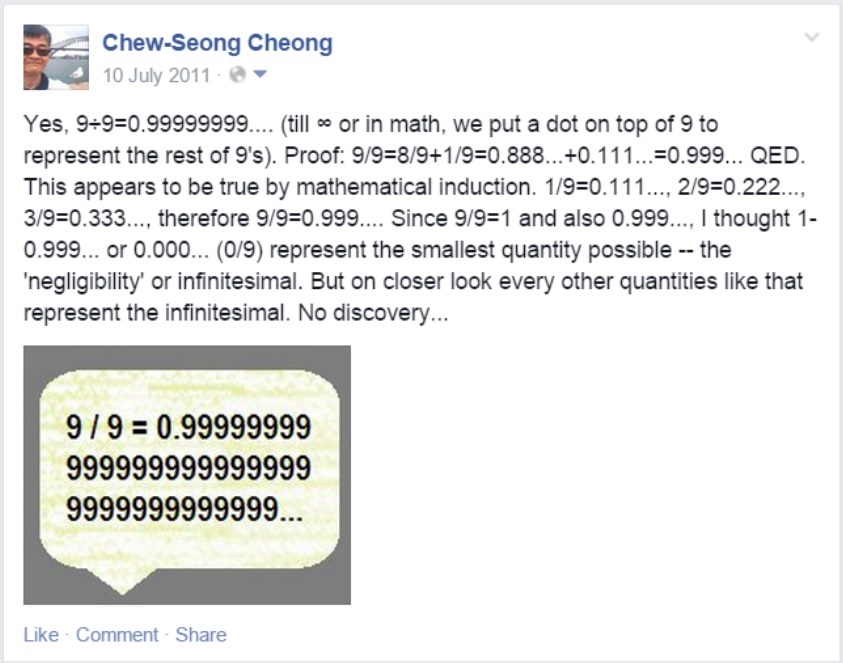 .
.
Moderator note:
How many other ways are there to prove this statement?
I don't particularly like this proof as 0.999... is not well defined. However, treating it as a geometric series and using the formula for such gives the result rigorously.
This is not induction.
Chew-Seong Cheong, Thank you, your explanation makes more sense to me than some of the earlier ones. With yours it's easier to accept that 1 is, in fact, the answer!
Sir, the inductive proof you have given seems to be incorrect, as it is an assumption you have that such a pattern continues throughout. My feeling is that it is no way related to Principle of Mathematical Induction and is just simple inductive reasoning, which may sometimes lead to wrong conclusions. This is from Wikipedia :
Inductive reasoning (as opposed to deductive reasoning or abductive reasoning) is reasoning in which the premises seek to supply strong evidence for (not absolute proof of) the truth of the conclusion. While the conclusion of a deductive argument is certain, the truth of the conclusion of an inductive argument is probable, based upon the evidence given.
Although its name may suggest otherwise, mathematical induction should not be misconstrued as a form of inductive reasoning (also see Problem of induction). Mathematical induction is an inference rule used in proofs. In mathematics, proofs including those using mathematical induction are examples of deductive reasoning, and inductive reasoning is excluded from proofs.
I am sorry for being critical (but I do appreciate your solutions a lot sir), but your first solution too has a problem. You have taken it as a lemma that 9 8 = 0 . 8 8 8 8 . . . . . and that 9 1 = 0 . 1 1 1 1 . . . . . . You need to provide the proofs of these lemmas you used too, to produce a complete solution.
There are many. From Wikipedia
Thanks Karthik Venkata and Pi Han Goh for the comments. Now I know what Mathematical Induction is. I was trained in electrical engineering and not math. I was quite lost in all these rules even as a student.
9/9 = 1 it does not equal 0.99999999. Just like 2/2, 8/8, and 16792745582/16792745582 all equal 1. Just as 1/1 does not equal 0.1111111111.
0.99999 is 0.99999 its not 1 and they're not equal simple as that
We're not talking about 0.99999
0 . 9 9 9 9 . . . = n = 0 ∑ ∞ 0 . 9 ( 0 . 1 ) n = 1 − 0 . 1 0 . 9 = 0 . 9 0 . 9 = 1
a good mathematical proof
1/3 =0.3333333333... 3/3=0.999999999999999.... 3/3 is a whole, therefore 1 making 0.99999... equal to 1
if 1/3 is 0.3(3), and 2/3 = 0.6(6) doesn't mean that 3/3 is 0.9(9). 0.6(6) is between 0.66 and 0.67, like 1/3 is between 1.33 and 1.34, these 3 parts adds together resulting 1 and not 0.9(9).
Let 0 . 9 9 9 9 9 9 9 9 . . . . = x .........(i)
Therefore, 1 0 x = 9 . 9 9 9 9 9 9 . . . . ......(ii)
Subtracting (i) from (ii)
9 x = 9
x = 1
Therefore, 0 . 9 9 9 9 9 . . . . = 1
QED.
That is so true I think .I still don't get it.
It can't be 1 it always tend to 1. One must understand the difference between tend to 1 and equal to 1 the difference is infinitely small. Therefore, we assume it to be 1 so the problem are solved eaisly but logically it is not equal to 1. Hence for this question answer should be "No."
While seemingly not the same. The numbers are mathematically inseperable, and therefore the same.
"Mathematically inseperable", what a perfect phrase. That sums up the entirety of this argument.
Both numbers would not be equal if there is a certain real number x such that 0 . 9 9 9 9 . . . . < x < 1 . Well, if you found one, you can argue that they are not equal but then again there is no such number. Hence, 0 . 9 9 9 9 . . = 1 .
1 − 0 . 9 = 0 . 1 1 − 0 . 9 9 = 0 . 0 1 1 − 0 . 9 9 9 = 0 . 0 0 1 ⋯ 1 − 0 . 9 9 9 . . . = 0 . 0 0 0 . . .
The one isn't there because there isn't an end of the zeroes where you can put it.
Alternatively, there are number systems with infinitesimals where 1 != 0.999...
Moderator note:
You have to be careful with justifying the claim of "there isn't an end of the zeroes where you can put it". How do you know that there isn't a "number" of the form 0 . 0 0 0 … 0 0 0 1 ?
Proof
(A) 9 0 . 9 ˉ = 0 . 1 ˉ
(B) But 0 . 1 ˉ = 9 1
From (A) and (B) , we get 9 0 . 9 ˉ = 9 1
Dividing both sides by 9, we get
0 . 9 ˉ = 1
A simple approach on this problem:
note that 1/3 = 0.3333...
now multiplying both parts by 3:
3 x 1/3 = 3 x 0.3333... , therefore 1 = 0.9999...
divide 3/3 in a calculator and see what the answer is
A calculator isn't as precise as a proof. It uses algorithms from a program, but is not absolutely correct. Also, showing that 3/3=1 does nothing for us, as it does not prove that 1 is the only form the answer may be written. Merely that it is the form the calculator is programmed to return. There have been multiple valid proofs here showing that they are equal. (Although I disagree with the precision in the "1/3=.333..." line of proving. The idea of setting x=.99.... And multiplying by 10, then solving the system of equations is simple yet elegant, and proves the validity absolutely without approximation. Likewise, the proof using summation notation sufficiently proves.
The trouble people are having is that infinitesimal distance between 0 . 9 9 9 9 … and 1 . The thing is, on the real number line, we don't have an infinitesimal quantity, only 0 or some other "concrete" nonzero, non-infinitesimal number. So that "infinitesimal" distance one speaks of is simply 0 , and we know that if a − b = 0 then straightforwardly we have a = b .
In fact, all real numbers are "approximated" by a sequence of rational numbers, by continued fractions or by decimal expansions (or any base of your choosing).
Let 0.9999....=x 10x=9.99.... 10x-x= 9=9x Therefore x=1
Reoeating decimals have a numerator that is the repeating digits and a denominator of as many 9s as there are digits that repeat. So in .9999.... the 9 repeats and there is only one digit that repeats (so one 9 in the denominator. So .9999...=9/9 and any fraction with the same numerator and denominator is equal to 1.
The problem I have with this proof is that although it is practically precise, it presupposes what we are trying to prove. How do we know that 1/3 strictly equals .3(3)? That is exactly what we want to prove, simply scaled. This introduces a clear fallacy. The simplest approach I have seen is letting x=.9(9), so 10x=9.9(9). So 10x-x=9.9(9)-.9(9), so 9x=9, so x=1. Therefore, 1=.9(9). There is no presupposition, simply the calling of a constant.
1/9 =0.1111111111......., 2/9=0.22222222222......., 3/9=0.33333333333........., etc 9/9=0.999999999................., and as we all know:9/9=1 :)
Go back to definition; see https://en.wikipedia.org/wiki/Decimal_representation
We have r=1 and 0.9999... corresponds to a0=0 and a_i=9 for each positive integer i. By definition, 0.9999... = 1.
Let x = 0.9999
then 10x = 9.9999
10x = 9+ 0.9999
10x = 9+x
9x=9
x=1
1 - 0.99999... = 0.00000....
Therefore 0.99999... Is equal to 1
1/9 is equal to 0.1111111.......... (1/9) * 9 = 9/9 = 1 = 0.999999999........
Similarly, if we take the repeating fraction method, for example 1/9,2/9,and 3/9,etc.. then .9999 must equal 9/9, which equals 1.
A slight variant that does not use limits and avoids the (correct but for some unintuitive) subtraction.
x=0.999... , 10x=9.999..., 10x=9+0.999... , 10x=9+x (no subtraction, just substitution...) , 9x=9 , x=1
You can also use ANY two fractions that add up to 1 and tha their decimal expansion often is 0.999... as in this example: 3/7 = 0.428571... and 4/7=0.571428.. adding the 3/7 and 4/7 gives 7/7=1 adding the decimals gives 0.428571... + 0.571428... = 0.999999... (no carry...ever) So once again.. 1=0.999...
Although i must confess I had answered as no and all my basics tell me that 0.999... and 1 are not equal but i can fault your solution
My teacher always used to explain me it this way :- If you don't believe 0.999...=1 Give me a a single number between 0.99... and 1
3 1 = . 3 3 3 . . . 3 ( 3 1 ) = . 9 9 9 . . . = 1
1/9=0.111... 9/9=0.999...=1 Or10*0.999... =9.999...,-0.999=9,/9=1
the simplest solution i know is: consider the equation
1/3 = 0.333333......
multiply both sides by 3
1 = 0.9999999........
1/3 = 0.33333...
3/3 = 1
1/3 * 3 = 3/3
0.3333...*3 = 0.999... ≈1
Set x = 0.999...
10x = 9.999...
10x - x = 9.999... - 0.999...
9x = 9.0
x = 1.0
0.999... = 1.0 Q.E.D.
Let x = 0.99999..........(1): 10x = 9.99999...........(2) : (2) - (1) gives, 9x =9. Therefore x = 9/9 = 1: So no gap between0.999999 and 1
Let k=0.999...9 -----(1)
=>10k=9.999...9 ----(2)
(2)-(1)
10k=9.999....9 -k = 0.99...9
9k=9.000...0=9 =>k=9/9=1
x=0.999... x=0.9+(0.1*x) hence x=1
Rounding up the figure 0.9999 to the nearest one's would be 1
This is what I was shown: Let R = 0.9999...... 10 R = 9.9999..... (10 R - R) (9.9999..... - 0.9999....) 9 R = 9 R = 1
does 1/3 = .333......? of so, then .999.... = 3/3 =1
Moderator note:
Great! Simple standard approach.
It does not tend to one, because tending to one means on a curve, the limit at point x approaches c and that point c is one. However you will never get a number like 0.9999999..... It will be like 0.999999999856782829 or whatever and then it will get infinitely closer to 1 but never at 0.999999999...... . simply put 0.9999999...... Never really actually happens..... Its just one
entre 1 et 0.999.. il existe aucun nombre , d'aprés la densité de Q dans R , 1=0.99..
0.99999....=0.9090....+0.0909.....=(10/11)+(1/11)=1
The difference between the is 0. Exactly 0.
Let 0.9999.....=m =>10m=9.9999....... =>9m+m=9.9999........ =>9m=9.9999...........-0.9999....... =>m=9/9 =>0.9999......=1
1/9=.11111 2/9 = .22222 3/9=.333333 . .
. 8/9=.888888 Then 9/9= .9999999 or 1?
We know 9/9 is equal to 1. but if if follows the pattern .999999 should be the answer. therefore .999999 = 1
Or a more simple approach. 1/3 = .3333... 1/3 * 3 = 1 .3333... * 3 = .9999...
If 0.333... = 1/3 is true then, 3 (0.333...) = 3(1/3) must also be true. We know that 3(1/3) = 1, then by transitivity law, 3(0.333...) = 1 must also be true. My former teacher in arithmetic, she has passed away 40 years ago anyway, told me that 3(0.333) = 0.999... And still, until now, I still don't know whether she is telling the truth. Maybe, my only mistake is that I will always keep on believing her that she was telling me the TRUTH.
0.9999... = 0.9 +0.09+0.009... (geometric series)
a=0.9
r=0.09/0.9 =0.1
Sn= a/1-r (sum to infinity)
=0.9/1-0.1
=0.9/0.9
=1
it may be tends to one. but practicaly its equal to one. and world is about practice , though the base is theory.
What is 0.999... subtracted from 1.000... .
We have:0.9999... = 0.1111.... x 9 Also: 0.1111.... = 1/9 -> 0.9999...= 1/9 x 9 = 1
1/3 = 0.3333... ; 3 * 0.3333... = 0.99999... ; 3 * 1/3 = 1 ; then, ; 0.99999... = 1
When people here say 0.99999....99 equals 1, is it true? I would say yes in mathematics, but it would not be true in real life. In chemistry, measuring something needs a lot of significant digits and repeat that work any times in order to get accurate data. in real life we don't really consider anything around be perfect either. This means that nothing is equal to something else!
3.333333.... = 1/3
3(3.333333... = 1/3)
9.999999... = 3/3
9.999999... = 1
There are an infinite amount of 9's. You can't add another 9 or stop at a certain number of 9's, it's forever. Which is almost incomprehensible and part of why this problem is so weird. With any finite number of 9's past the decimal the number is aproximatly 1, but with an infinite number of 9's, it is equal to 1.
simply round 0.9999..
Yes. It is like saying that 1/3 is 0.333333333333333333333333333333333333333...
0.3333...=1/3 0.3333...x3=3x1/3 No carry over numbers since example 0.333x3=0.999 0.9999...=3/3=1
There is a property of real numbers that between any two distinct real numbers, there would be infinite real numbers. And between 0.9999...... and 1, there is no other distinct real number which makes both of them equal.
0.33333... = 1/3 3*0.3333...=3/3 = 0.999999 = 1
Since 8/9=0.888..., then 0.999...=9/9. If the denominator and the numerator is the same, then 9/9 would be 1. Therefore, 0.999...=1.
PROOF 3 1 = 0 . 3 3 3 . . . 3 1 + 3 1 + 3 1 = 0 . 9 9 9 . . . 3 1 + 3 1 + 3 1 = 1 0 . 9 9 9 . . . = 3 1 + 3 1 + 3 1 = 1
Q.E.D.
0.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,IS ,,,,,,,,,,,SIMPLY =1
A simple proof that while not exceptionally rigorous, serves to illustrate the point is:
1/3=.3333.... 2/3=.6666.... 1/3+2/3=.9999... Or 1. This is the algebraic method for demonstrating. It holds true only when you take all repeating digits to infinity. Should you stop at any point before then, it is not 1, but a finite number. To infinity!
1 / 3 = 0.33333 0.33333 * 3 = 0.99999 Therefore 0.99999 = 1
I don't think we can say they are typically same, but we can say it tends to 1. However for simplicity we can take as they are equal.
I agree with Solution given by Karthik Venkata which is easiest to understand and Okay.
0.999999......=(9/10)+(9/10^2)+(9/10^3)+...(9/10^n) where lim n->Inf
0.333333.....=(3/10)+(3/10^2)+(3/10^3)+...(3/10^n) where lim n-> inf also =1/3
3(1/3) = 3((3/10)+....3(3/10^n) where lim n->inf
3/3 = 9/10+....(9/10^n) where lim n-> inf
1 =0.99999999
1/3 = .3333... .3333..... 3=.9999... .9999...=1/3 3=1
One thing is not = to another, unless it is the absolute equal. Everything else is just argument to try to prove the contrary.
It's easy.... .9999 does not always equal 1. In some permutations it is may be correct . In some it is clearly not. Math should be an absolute not an estimation.
I've got some bad news about irrational numbers. Given that the fraction 1/3 has an infinite number of .3333... As 3x.3333.... approaches infinity, it is equal to 1.
PROOF
Let 0 . 9 9 9 9 . . . . = x . Then 1 0 x = 9 . 9 9 9 9 . . . . .
Now subtracting the first equation from the second, 9 x = 9 ⇒ x = 1 ⇒ 0 . 9 9 9 9 . . . . = 1
Q.E.D.