Zi Song Polynomial

Let $m= \deg f(x)$ . Then, note that $\deg f(f(x))= m^2$ . Since $2$ is not a perfect square, $\deg f(f(x)) \neq 2$ , and hence $\deg (f(f(x)) - x^2)= \max (m, 2)$ . Also, note that $\deg (xf(x))= m+1$ .

If $m \geq 2$ , $\deg (f(f(x))-x^2)=m$ . Equating the degrees, $m^2= m+1$ and because it has no integer roots, a contradiction. So $m < 2$ , and $\deg (f(f(x))-x^2)= 2$ . Equating the degrees, $m+1= 2 \implies m=1$ . So $f(x)$ is a linear polynomial.

Let $f(x)= ax+b$ , so $f(f(x))-x^2= a(ax+b)+b-x^2= -x^2+a^2x+(ab+b)$ And $xf(x)= x(ax+b)= ax^2+bx$

Comparing the coefficients of $x^2$ , $a = -1$ Comparing the coefficients of $x$ , $a^2= b \implies b= 1$ We thus get the polynomial $f(x)=1-x$ . It can easily be verified that this polynomial indeed satisfies the given conditions: $f(f(x))-x^2 = 1-(1-x)-x^2= x-x^2= x(1-x)= xf(x)$ Our desired answer is $f(-100)= 1-(-100)= \boxed{101}$ .

It is easy to check that no constant polynomial can satisfy the equation, since that implies that $x^2 +kx - k = 0$ for all $x$ .

Let $k>0$ be the degree of $f(x)$ . Then the degree of $f(f(x)) - x^{2}$ is $\max (k^{2}, 2)$ , and the degree of $xf(x)$ is $k + 1$ . These degrees must be equal.

Case 1. $\max (k^{2}, 2)=k^2$ . In this case, $k \geq 2$ . By equating the degrees, we obtain $k^{2} = k + 1$ , which has no solution in positive integers.

Case 2. $\max (k^{2}, 2)=2$ . In this case, we obtain $k + 1 = 2$ , and therefore $k = 1$ . Let $f(x) = ax + b$ . Substituting and solving yields $f(x) = 1 - x$ , so $f(-100) = 101$ .

Let's denote $deg(f(x))=d$ . Since there is a $-x^2$ term on the LHS, we would wanna know whether it will affect the degree of the whole expression on the LHS.

For $d\geq 2$ , $deg(ff(x)) = d^2 \geq 4 > 2$ . So the $-x^2$ term will not affect the degree of the expression on LHS. Equating the degrees of the equation, $d^2 = d+1$ $d =\frac {1\pm \sqrt {(-1)^2 -4(1)(-1)}}{2(1)}$ where there are no integer solutions. Thus for all $d \geq 2$ , they do not satisfy the equation.

For $d=1$ , $deg(ff(x)) = 1 < 2$ . So the degree of LHS is 2, equating the degrees, $2 = 1+1 \Rightarrow$ TRUE $\Rightarrow deg(f(x))=1$ $f(x) = ax+b$ Substituting back to the given equation, $a(ax+b) +b - x^2 = x(ax+b)$ $-x^2 +a^2x + ab+b = ax^2+bx$ Comparing constants, $ab+b=0$ $b(a+1)=0$ $a=-1, b=0$ Comparing coefficient of $x^2$ , $a=-1$ where it also satisfy the constant's equation above. Comparing coefficient of $x$ , $a^2=b$ $b=(-1)^2$ $b=1$ So we get $f(x) = -x +1$ , $f(-100) = -(-100) +1=101$

let $f(x) = -100$ , then $f(-100) = x$

so $f(f(x))-x^{2}=xf(x)$

$f(-100)=x(-100)+x^{2}$

$x=x^{2}-100x$

$x^{2}=101x$

$x=101$

$f(-100)=\boxed{101}$

In these situations with a generalize polynomial, it is best to see if we can narrow down the possibilities for the polynomial.

Let $n$ be the degree of the polynomial $f(x)$ . If $n > 2$ , then the degree of the terms on the left is $n$ and on the right is $n+1$ , so its impossible for that to occur and still hold for all values of $x$ .

If $n=2$ and $n$ is monic, then the left has degree 1 and the right has degree 3. Again, impossible by our constraints. Even if $n$ is not monic, the degrees turn out to be 2 on the left and 3 on the right, which is still unequal.

The last, and feasible option, is for $f(x)$ to be linear. If it is linear, then the degree of the terms on both the left and right is 2.

Let $f(x)=ax+b$ , so that the given equation eventually simplifies down to $x^2(-a-1) + x(a^2 - b) + (ab+b) = 0$ (I won't bother you with all the simplification.) For the two sides to be equal for any value of $x$ , the coefficients of the terms with $x$ and the constant term must be zero. It becomes clear that for this to occur, $a=-1$ and $b=1$ , so our polynomial becomes $f(x)=-x + 1$ , and the desired answer of $101$ follows.

f(x)=1-x satisfies this equation. Plugging in -100 yields $\boxed{101}$

$deg(LHS) = deg(RHS)$

If $deg(f) = n$ ,

then $max(2n, 2) = n + 1 \Rightarrow n = 1$

then $f(x) = ax + b$

$f'(x) = a$

Differentiating both sides,

$f'(f(x)) * f'(x) - 2x = f(x) + x * f'(x)$

$\Rightarrow a^2 = 2x + ax + b + ax$

$\Rightarrow (a^2 - b) = 2x(a + 1)$

Equating coefficients of x and 1,

$a = -1, b = a^2 = 1$

$\Rightarrow f(x) = 1 - x$

$\Rightarrow f(-100) = 101$

f(f(x)) = x^2 + xf(x). For the ques to be true for all x, value of expression at RHS = LHS. if f(x) is a polynomial of degree>1, f(f(x)) will always have degree > degree of xf(x) and RHS not equals LHS. But if f(x) is a linear function, then f(f(x)) is also linear but xf(x) will be a quadratic. So, we need to remove x^2 from RHS. This can be done by taking f(x)= k-x, for some constant k. Hence, f(fx))= x and xf(x)= kx-x^2. so, RHS= kx and LHS=x. Hence, k=1 and f(x)=1-x !!!!!!

This problem yields easily to a symbolic solution that parallels that of Sreejato Bhattacharya, except that it's unnecessary to determine the degree of the $f(.)$ . It's simply a matter of defining the function with successively higher degrees until one of them 'works'.

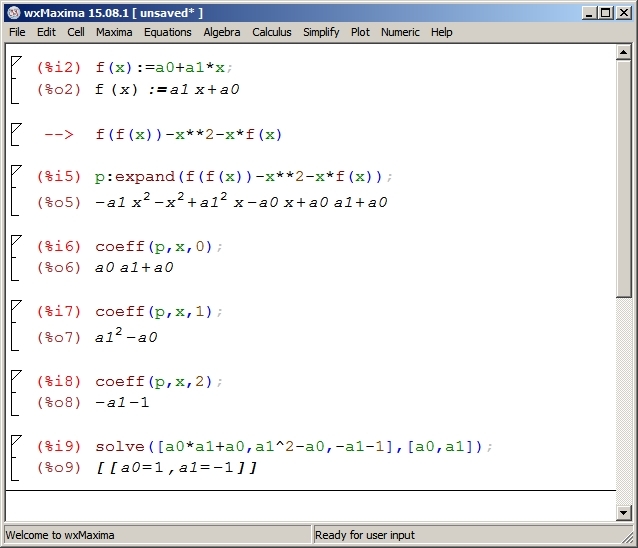
Of course the algebra software has to be up to the task. I first used sympy for this. It couldn't fully solve the equations even for the linear possibility for $f(.)$ . When I tried using it to solve the equations for higher degrees it seemed to go into infinite loops.

Yay! I got a level 5 problem right! Unfortunately, I accidentally put in -99 first for some reason, so I lost a bit of points. Anyway.

Let us first discuss which degree the polynomial $f(x)$ can be. Notice that the left side of the equality has the degree $max(n^2, 2)$ , where $n = deg f(x)$ (if the degree of $f(x)$ is 0 or 1, the highest degree will be the term $-x^2$ . Otherwise, the highest degree will be the square of the degree of the polynomial), while the degree of the right side is $n+1$ , so we're looking for an $n$ for which $max(n^2, 2) = n+1$ . $n = 0$ does not satisfy the conditions, while $n = 1$ does. For $n \geqslant 2$ , $n^2 > n+1$ , so $deg f(x)$ can only be 1.

Now, $f(x) = ax + b$ . By inserting this in the equality, we get $-x^2 + a^2x + a(b+1) = ax^2 + bx$ . Since this must hold for all $x \in \mathbb{R}$ , all corresponding degrees on each side must be equal, so we get $a = -1$ for the second degree, $a^2 = b$ for the first degree and $a(b+1) = 0$ for the degree 0. By plugging $a = -1$ into either of the latter two equations we get $b = 1$ .

$f(x) = -x + 1$ , so $f(-100) = -(-100)+ 1 = 101$

Let f(x) = ax+b since given equation has power of x upto 2. Now if we substitute f(x) and equate coefficiants of x and x^2 we get a = -1 , b = 1. Therefore f(x) = -x+1 and we get f(-100) = 101

In order for this relation to be satisfied, $f(x)$ must be a linear function (note that if $f$ is a quadratic the left side is of degree 4 and the right side of degree 3, and if $f$ is constant the left side is of degree 2 and the right side of degree 1). So we have $a(ax+b) + b - x^2 = ax^2 + bx$ . From this, we gather $a=-1, b=1$ , so $f(x) = -x+1$ . Hence, $f(-100) = \boxed{101}$

Assume FX to be (-x+n) so degree of eq on lhs and rhs be same solving we get n=1 plug in -100 to get 101.

Assume (a) to be a solution of f(x) , so $f(a)=0$

$\because \quad f(f(x))-{ x }^{ 2 }=xf(x) ........ (1)$

by putting $x=a$ , and $f(a)=0$

we get $f(0)-a^2=0$ , so $\boxed { f(0)={ a }^{ 2 } }$

by putting $x=0$ in equation 1, we have $\boxed { f({ a }^{ 2 })=0 }$

by putting $x=a^2$ in equation 1, and by using the two boxed results, we have $a^2-a^4=0$

whose solutions are: $\boxed { a=0,-1,1 }$

now we check the validity of the three possible solutions:

it's very obvious that $a=-1,1$ contradicts the solution $a=0$ . this can be checked by substituting $a=\pm 1$ and $f(\pm 1)=0$ in equation 1 the result is that $f(0)=1\neq 0$ so we have to refuse one of the two sets. no hard work need to be done to show that $a=0$ is a refused solution. because $f(x)=x$ doesn't satisfy equation 1.

now we have $f(0)=1$ , and $f(\pm 1)=0$

one final note is that the solution $a=-1$ raises the power of f(x) to 2 (i.e. $f(x)=1-{ x }^{ 2 }$ ), and consequently the power of $f(f(x))$ to 4. which doesn't satisfy equation 1. whose R.H.S term is of order 3 only. so we have to refuse one of the two solutions, namely $a=-1$ or $a=1$

to guarantee that $f(0)$ is satisfied, we have to refuse $a=-1$ , so that the solution $( a=1 )$ takes the form: $f(x)=1-x$ , which satisfies all previous conditions

so, $f(x)=1-x$

and $\boxed { f(-100)=101 }$

F(x)= (-x+1)...It came to me after I saw equation..

I just let $f (x)=x$ to get a quadratic equation of $f (x)$
just swapping $x$ and $f(x)$ gives us $(f (x))^2+(x-1)f (x)=0$
which gives f (x)=1-x; since f (x) is not equal to 0...now just plugging in -100 gives the result....I'm not sure if there is any fault in this process...if there is any, please help me find it out....

Let f(x) = x; ......(i)
Then f(f(x))= f(x)
f(x) -x² = x* x ;
f(x) = 2x²
2x² = x. [Eq. (I) f(x) =x]
x= 1/2 ; f(1/2) = 1/2
f[f(x)] - x² = xf(x)
Now let f(x) =y
f(y) - x² = xy
Put y= 1/2
f(1/2) - x² = x/2
(1/2) - x² = x/2. ; therefore x= 1/2 or -1
f(y) = (1+2y)/4 or 1-y
f(-100) = -199/4 or 101
f(x) can not be negative due to equal of 2x²
So answer is 101